Как найти площадь треугольника

Есть несколько способов найти площадь треугольника. Для этого можно воспользоваться формулами или специальными сервисами, которые помогут рассчитать площадь онлайн быстро и просто.

Мы расскажем, как найти площадь треугольника, какие применяются формулы, какими онлайн-калькуляторами можно воспользоваться для проведения вычислений.

Что такое треугольник

Понятие геометрических фигур начинают изучать в 3 классе. В соответствии с учебным материалом треугольник – это геометрическая фигура, состоящая из трех точек, которые не лежат на одной прямой и трех отрезков, которые последовательно соединяют эти точки и ограниченной ними части плоскости.

Из чего состоит треугольник:

• Вершины треугольника – это точки, которые соединяются отрезками.
• Стороны треугольника – это отрезки, соединяющие точки.
• Угол треугольника – это фигура, образованная двумя отрезками, выходящими из одной точки.

Виды треугольников:

• По сторонам: разносторонний, равнобедренный (когда равны две стороны), равносторонний (когда равны все стороны);
• По углам: остроугольный, тупоугольный, прямоугольный.

Характеристики треугольников, которые применяются при расчете его площади:

• Высота – перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
• Периметр – сумма длин сторон треугольника.
• Вписанная окружность – это окружность, лежащая внутри треугольника, касающаяся всех его сторон.
• Описанная окружность – это окружность, на которой лежат все вершины треугольника.

Что такое площадь треугольника

Площадь треугольника — это величина той части плоскости, которую он занимает. За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Например, если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной 1 см.

Как найти площадь треугольника

Есть несколько способов найти площадь треугольника. В зависимости от вида фигуры, от того, какие есть вводные данные, применяются разные формулы.

Основная формула звучит так: площадь треугольника равна половине произведения длины высоты треугольника и длины стороны, к которой проведена высота.

Формулы

Универсальные

Сначала рассмотрим универсальные формулы, подходящие для треугольников любых видов.

1. Основная формула: Площадь треугольника, если известны основание (любая сторона) и высота (проведенная к этому основанию)

S = a * h / 2.

Где:

• а – любая сторона;
• h – высота, проведенная к стороне а.

2. Формула Герона

S = √ (p * (p - a) * (p - b) *(p - c)),

Где:

• а – сторона треугольника;
• b – сторона треугольника;
• с – сторона треугольника;
• p = (a + b + c) / 2 — полупериметр.

3. Площадь треугольника через две стороны и угол между ними

S = (a * b * sinα) / 2

где:

• а – сторона треугольника;
• b – сторона треугольника;
• α – угол между сторонами.

4. Площадь треугольника через радиус вписанной окружности и сторон

S = r * (a + b + c) / 2.

Где:

• а – сторона треугольника;
• b – сторона треугольника;
• с – сторона треугольника;
• r – радиус вписанной окружности.

5. Площадь треугольника через радиус описанной окружности и стороны

S = (a * b * c) / 4R.

Где:

• а – сторона треугольника;
• b – сторона треугольника;
• с – сторона треугольника;
• R – радиус описанной окружности.

6. Площадь треугольника по стороне и двум прилежащим углам

S = (a²* sinα * sinβ) / (2 * sin (α + β)).

Где:

• а – сторона треугольника;
• α – прилежащий угол;
• β – прилежащий угол.

Для равностороннего треугольника

Равносторонним треугольником называют треугольник, чьи стороны равны.

Формулы расчета площади при равностороннем треугольнике:

1. Расчет площади через высоту

S = h2 / √3

Где h– высота треугольника.

2. Расчет площади через сторону

S = (√3 * a2) / 4.

Поскольку в равностороннем треугольнике все стороны равны, то можно найти площадь, зная всего одну сторону.

3. Расчет площади через радиус вписанной окружности

S = 3 √3 * r2.

r – радиус вписанной окружности.

4. Расчет площади через радиус описанной окружности

S = (3√3 * R2) / 4

R – радиус описанной окружности.

Для равнобедренного треугольника

Основное свойство равнобедренных треугольников: две его стороны равны.

Формула расчета площади равнобедренного треугольника:

Площадь треугольника через боковые стороны и угол между ними

S = (a²* sinα) / 2.

Поскольку в равнобедренном треугольнике боковые стороны равны, для расчета можно взять одну из сторон – а и α – угол между ними.

Для прямоугольного треугольника

В чем особенности прямоугольного треугольника:

• Наличие прямого угла.
• К прямому углу прилегают 2 катета a и b.
• Самая длинная сторона треугольника гипотенуза – с.

Формулы расчета площади прямоугольного треугольника:

1. Расчет площади через катеты

S = a * в / 2.

Где а и в – катеты треугольника.

2. Расчет площади по гипотенузе и острому углу

S = (c2 * sin(2α)) / 4.

Где:

• с – гипотенуза;
• α – величина прилегающего к ней угла.

3. Расчет площади по катету и прилежащему углу

S = (a2 * tgα) / 2.

Где:

• а – катет;
• α – угол между этим катетом и гипотенузой.

4. Расчет площади с применением формулы Герона

S = √(p * (p - a) * (p - b) * (p - c))

Где:

• а, b, c – стороны треугольника;
• p = (a + b + c) / 2 — полупериметр.

5. Расчет площади через гипотенузу и радиус вписанной окружности

S = r * (r + c).

Где:

• r – радиус окружности;
• с – гипотенуза.

6. Расчет площади по отрезкам, на которые делит вписанная окружность его гипотенузу

S = c1 * c2

c1 и c2 – отрезки, на которые разделена гипотенуза точкой соприкосновения со вписанной окружностью.

Примеры и задачи на вычисление

Приведем несколько задач с решением на вычисление площади треугольника.

1. Найдем площадь треугольника со стороной 16 см. и высотой, проведенной к данной стороне 19 см.
   
   
   

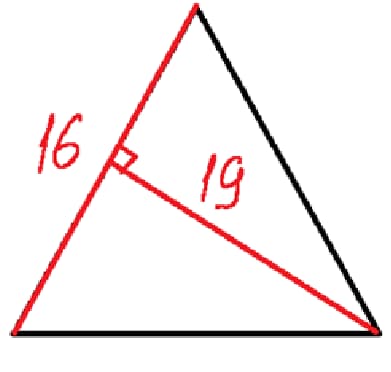
   Решение

   Применим основную формулу: S = a * h / 2.

   S=16 * 19/2=152

   Ответ 152 см²

2. Найдем площадь прямоугольного треугольника, если его катет равен 16см., а гипотенуза 20 см.
   
   
   

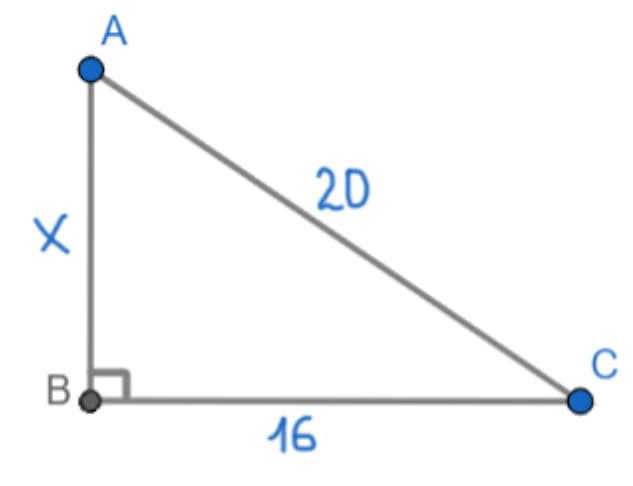
   Решение:

   В прямоугольном треугольнике любой катет является высотой. Высотой может быть сторона AB, а основанием сторона ВС.

   Для вычисления стороны АВ воспользуемся теоремой Пифагора:

   х² + 16² = 20²

   x² = 400–256 = 144

   x = 12

   Воспользуемся основной формулой нахождения площади прямоугольных треугольников:

   S = 0,5 * 12 * 16 = 6 * 16 = 96

   Ответ: 96 см².

3. Дан равнобедренный треугольник ABC (AB = BC). Угол при основании равен 15°. Боковая сторона равна 10. Требуется рассчитать площадь треугольника ABC.
   
   

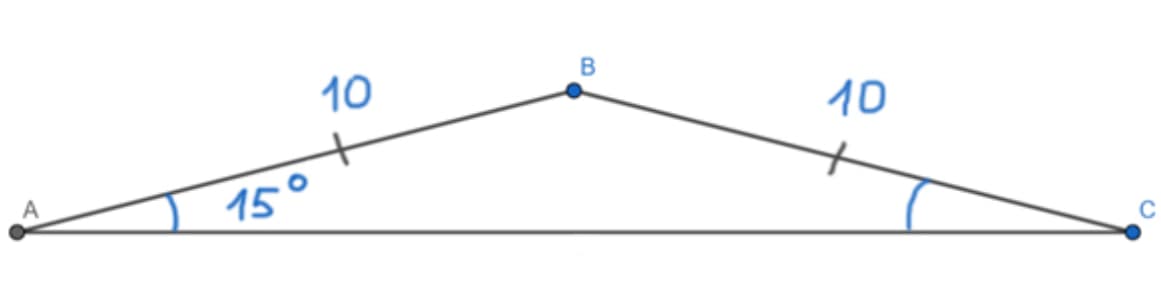
   Решение

   Нам даны две боковые стороны треугольника. Нужно найти синус угла между ними.

   В равнобедренном треугольнике углы при основании равны, отсюда следует:

   ∠ABC + ∠ВАС + ∠BCA = 180°

   ∠ABC = 180° - ∠ВАС - ∠BCA

   ∠ABC = 180° - 15° - 15° = 150°

   Таким образом, синус угла АВС 150° равен sin(150°) = sin(30°) = 0,5.

   Подставляем данные в формулу:

   S = 0,5 * AB*BC * sin(∠ABC)

   S = 0,5 * 10*10 * 0,5 = 25

   Ответ: 25

Калькуляторы онлайн – обзор сервисов

Для расчета площади треугольников можно воспользоваться специальными калькуляторами, которые предлагают специальные сервисы. Мы сделали обзор самых удобных и популярных онлайн-калькуляторов.

calc.by

Сalc.by поможет быстро найти площадь треугольника разными способами в зависимости от известных данных. Калькулятор показывает подробное решение, поэтому его можно применять для проверки своих вычислений.

Применяемые формулы расчета площади:

• через основание и высоту;
• по трем сторонам (формула Герона);
• через две стороны и угол;
• через радиус вписанной окружности;
• через радиус описанной окружности.

skysmart.ru

Используя этот онлайн калькулятор, вы сможете найти площадь треугольника по:

• трем сторонам;
• двум сторонам и углу между ними;
• по стороне и опущенной на нее высоте.

kalk.top

Калькулятор поможет вычислить площадь треугольника по трем сторонам и по основанию и высоте.

FAQ

Кто первым начал вычислять площадь треугольника?

Первым точную формулу площади треугольника применил Герон Александрийский. Это греческий математик, живший в I веке н. э. Формула, которую он применил, так и называется формула Герона.

Почему важно уметь вычислять площадь треугольника?

Умение вычислять площадь треугольника важно при решении различных задач в математике и научных исследованиях. Умение вычислять площадь треугольника также является полезным и в повседневной жизни. Это может пригодиться в строительстве, архитектуре, инженерии, дизайне и т. д.

Например, рассчитав площадь треугольника, вы сможете узнать, сколько вам потребуется материала для изготовления треугольного объекта, узнаете площадь земельного участка для постройки клумбы или целого дома.

Вывод

• Площадь треугольника является одним из базовых понятий геометрии.
• Знать и уметь вычислять площадь треугольника полезно не только школьникам для успешной аттестации, но и всем взрослым в повседневной жизни.
• Для расчета площади можно воспользоваться специальными онлайн-калькуляторами, но полезнее знать и понимать формулы расчета.
• В зависимости от исходных данных применяют разные формулы вычисления площади.
• Основная формула для вычисления площади треугольника: S = a * h / 2. Где: а – любая сторона; h – высота, проведенная к стороне а.