Как найти периметр квадрата
Впервые школьники знакомятся с понятием периметра в начальной школе. Как правило, они учатся находить его на примере правильных фигур, стороны которых равны. Поэтому ученикам рекомендуется начать изучение темы с вопроса о том, как найти периметр квадрата.
Периметр квадрата – основные определения
Прежде чем совершать математические расчёты, следует разобраться в основных понятиях: какую фигуру называют квадратом и что такое периметр.
Квадрат — это замкнутая 2-мерная фигура в форме правильного четырёхугольника, который имеет равные стороны и углы. Иными словами, он имеет 4 стороны одинаковой длины, 4 прямые угла.
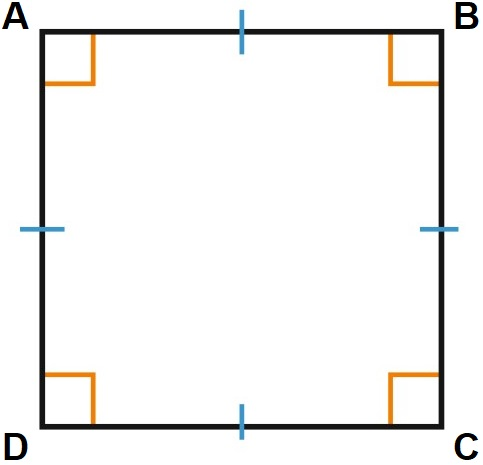
Одной из фундаментальных характеристик квадрата является периметр – общая длина границы фигуры, или сумма длин всех её сторон.
Знать, как вычислять периметр квадрата, полезно в разных ситуациях. Например, это важно в строительстве (при расчёте материалов на ограждение), в спорте (при расчёте дистанции бега) и пр. В то же время периметр, являясь базовым измерением, позволяет производить более сложные расчёты: находить площадь фигуры, длину вписанной или описанной окружности и пр.
Как найти периметр квадрата
В математике используются 2 основные формулы определения периметра квадрата. В первом случае его находят через длины сторон, во втором – через длину диагонали фигуры.
Самый простой способ найти периметр квадрата – сложить длины всех его сторон. И это можно сделать, зная параметры одной стороны. Периметр квадрата ABCD с заданной стороной a рассчитывается по формуле:
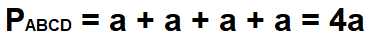
Периметр квадрата ABCD с заданной диагональю d рассчитывается по формуле:
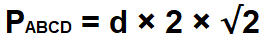
Разберем примеры – задачи и решение
Задача №1. Вычисление периметра квадрата
Сторона квадрата равна 14,5 см. Каков периметр фигуры?
Решение:
Поскольку в квадрате все стороны равны, то находим периметр по формуле: P = 4a = 14,5 x 4 = 58 см.
Ответ: 58 см.
Задача №2. Сравнение периметров фигур
Какой земельный участок потребует установки большей ограды: квадратный со стороной 15 м, или прямоугольный со смежным сторонами 18,5 м и 15,5 м?
Решение:
Сначала находим периметр квадратного участка земли: P1 = 15 x 4 = 60 м.
Находим периметр прямоугольного участка: P2 = 2 x (18,5 + 15,5) = 68 м.
Граница прямоугольного участка длиннее. Вычисляем разницу периметров: P2 – P1 = 68 – 60 = 8 м.
Ответ: периметр прямоугольного участка больше периметра квадратного участка и потребует установки ограды длиннее на 8 м.
Задача №3. Вычисление периметра сложной фигуры
Получена схема фигуры, составленной из 2 квадратов. Каков периметр этой фигуры?
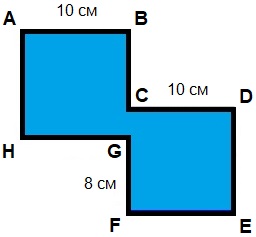
Решение:
Квадраты, образующие сложную фигуру, не пересекаются, т.к. их параллельные стороны равны 10 см. Однако они имеют общую часть стороны; находим её: CG = DE – GF = 10 – 8 = 2 см.
Теперь находим неизвестную часть границы фигуры: BC = 10 – 2 = 8 см.
Находим периметр: PABCDEFGH = AB + BC + CD + DE + EF + FG + GH + HA = 10 + 8 + 10 + 10 + 10 + 8 + 10 + 10 = 76 см.
Сначала вычислим длину BC. Так как каждая сторона квадратов равна 10 см и часть правого квадрата равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.
Ответ: 76 см.
FAQ
В каких единицах измеряется периметр квадрата?
Периметр квадрата, как и любой геометрической фигуры, измеряется в стандартных величинах: миллиметрах, сантиметрах, метрах и пр.
Как связаны площадь и периметр квадрата?
Периметр – это общая длина всех сторон квадрата (измеряется в единицах), а площадь – это величина пространства внутри фигуры (измеряется в квадратных единицах). Они представляют собой разные части квадрата, но для нахождения обоих требуется знать длину 1 стороны.
Находить периметр любых четырёхугольников настолько же легко, как находить периметр квадрата?
Как и в случае с квадратом, периметр четырёхугольника находится путём сложения длин всех сторон. Однако нужно учесть, что если фигура не является квадратом или правильным ромбом, то не все её стороны равны.
Вывод
Периметр квадрата, как и любой 2-мерной замкнутой фигуры, определяется как общая длина его границы. Поэтому самым простым способом найти этот параметр является сложение всех его сторон.
Поскольку квадрат – это очень простая и правильная фигура, школьникам младших классов рекомендуется решать задачи на нахождение его периметра, чтобы освоить эту тему. Затем можно переходить к более сложным упражнениям – нахождению периметров неправильных четырёхугольников.
