Как найти периметр

Когда школьники начинают осваивать уроки математики, им кажется, что периметр – это что-то сложное и непонятное, а найти его очень сложно. На самом деле это не так.

В этой статье мы расскажем, что такое периметр, разберем как его найти для различных фигур и на примере решения задач покажем, что данное вычисление не несет в себе никаких сложностей.

Что такое периметр

Периметр – это сумма длин всех сторон фигуры. В математике и геометрии периметр является одним из основных понятий, и играет важную роль при изучении различных фигур, таких как круги, треугольники, прямоугольники и многоугольники.

В реальной жизни это знание поможет при строительстве домов или установке заборов., ведь для этого необходимо уметь вычислять периметр участка земли, чтобы определить количество материала, необходимого для работ.

Периметр обозначается латинской буквой Р. Обычно, под этой буквой пишут наименование фигуры, например Р_круга, Р_{квадрата}, Р_{треугольника} и т.д.

В разных системах могут использоваться разные единицы для измерения периметра. Вот некоторые из них:

1. Система метрических единиц:
• Метр (м): основная единица измерения длины в метрической системе. Периметр обычно измеряется в метрах.
• Километр (км): 1 километр равен 1000 метров. Чтобы перевести метры в километры, нужно разделить число метров на 1000.
• Сантиметр (см): 1 сантиметр равен 0,01 метра. Чтобы перевести метры в
2. Система английских единиц:
• Фут (ft): основная единица измерения длины в системе английских единиц. 1 фут равен 0,3048 метра. Чтобы перевести метры в футы, нужно разделить число метров на 0,3048.
• Ярд (yd): 1 ярд равен 3 футам или около 0,9144 метра. Чтобы перевести метры в ярды, нужно разделить число метров на 0,9144.
• Миля (ми): 1 миля равна 1760 ярдам или приблизительно 1,60934 километра. Чтобы перевести метры в мили, нужно разделить число метров на 1609,34.

Когда у вас есть значение периметра в одной единице, вы можете использовать указанные преобразования, чтобы перевести его в другие единицы измерения. Это позволит вам представить периметр в удобной для вас форме, в зависимости от системы измерения, которую вы предпочитаете использовать.

В России для вычисления периметров используется метрическая система.

Формулы нахождения периметра

Формулы нахождения периметра меняются, в зависимости от фигуры. Для простых фигур вычисление будет легким, для сложных – более трудоемким.

Разберем подробнее как вычислять периметр под любую геометрическую фигуру.

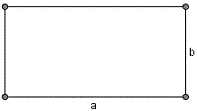
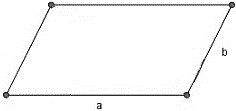
Прямоугольник и параллелограмм

У данных фигур равны противоположные стороны, из чего следует, что периметр будет равен сумме двух сторон, умноженных на 2:

P = 2 * (a + b), где а и b – соседние стороны фигуры.

Прямоугольник:

Параллелограмм:

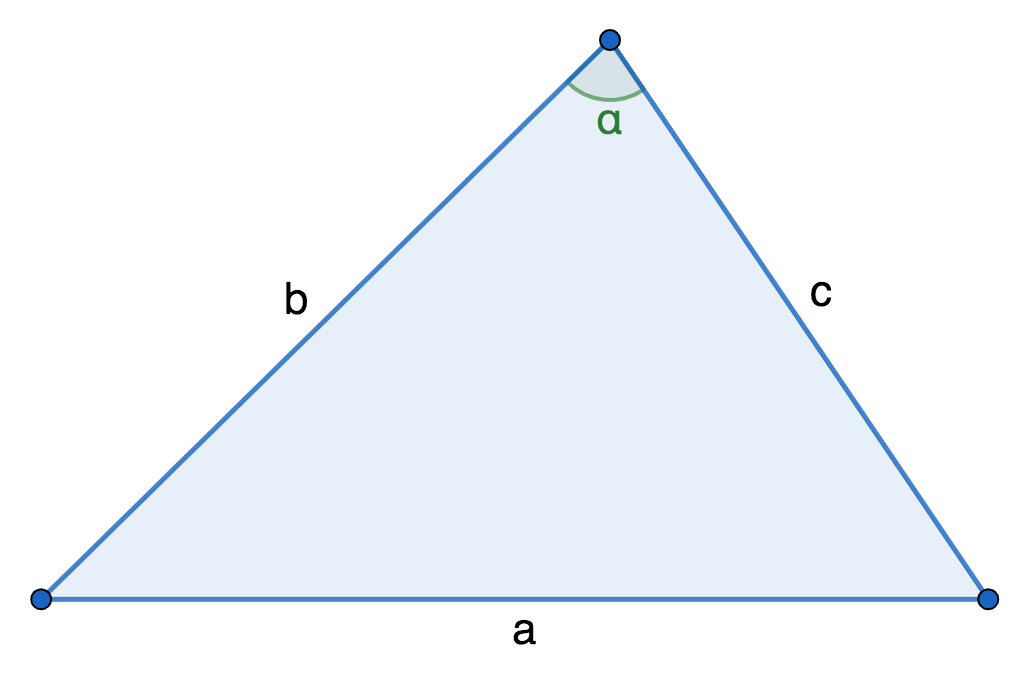
Треугольник

Периметр треугольника равен сумме длин его сторон:

P = a + b + c, где a, b, c – длины сторон треугольника.

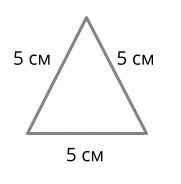
Равносторонний треугольник

У этой фигуры все стороны равны, следовательно периметр равен произведению длины стороны на количество сторон, т.е. на 3:

P = a * 3, где а – длина одной стороны.

Квадрат и ромб

У квадрата и ромба длины все стороны равны, следовательно периметр равен произведению длины стороны на количество сторон, в данном случае на 4:

P = a * 4, где a – длина одной из сторон.

Исходя из этой формулы, можно понять, что периметр любых равносторонних многоугольников будет вычисляться как:

P = a * n, где a – длина одной стороны, n – количество сторон.

Примеры решения задач

Разберем несколько примеров задач на вычисление периметра.

Пример 1

Дано: Равносторонний треугольник имеет стороны равные 12 см.

Найти: периметр равностороннего треугольника.

Решение:

Исходя из формулы вычисления периметра равностороннего треугольника P = a * 3 мы получаем следующее уравнение:

P = 12 * 3

P = 36 см.

Ответ: периметр равностороннего треугольника равен 36 см.

Пример 2

Дано: прямоугольник имеет периметр равный 40 см, и длину одной стороны – 6 см.

Найти: длину второй стороны.

Решение:

Исходя из формулы вычисления периметра прямоугольника P = 2 * (a + b) мы знаем, что периметр – это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания – получим сумму двух оставшихся сторон:

40 = 2 * (6 + b)

20 = 6 + b

b = 14 см.

Ответ: длина второй стороны прямоугольника равна 14 см.

Онлайн-калькуляторы для вычисления периметра

Существуют сайты, на которых вы можете вычислить периметр любой фигуры, лишь вводя данные сторон в активную строку. Мы собрали несколько самых популярных платформ:

• AllCalc – на странице предлагается набор онлайн калькуляторов, позволяющий вычислять периметр для основных геометрических фигур. Также, есть программы для вычисления длин окружности и дуги.
• Калькулятор – позволяет несколькими способами рассчитать периметры различных геометрических фигур, таких как квадрат, прямоугольник, треугольник, круг.
• OnlineMSchool – вычисляет периметры таких фигур как, треугольник, квадрат, прямоугольник, параллелограмм, ромб, трапеция.

FAQ

Могу ли я самостоятельно понять тему периметра?

Конечно да, в нашей статье есть все необходимые формулы для новичков в мире математики.

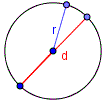
Есть ли периметр у окружности?

У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус.

Длина окружности – это произведение числа π на два радиуса или произведение π на диаметр:

L = d * π = 2 * r * π, где d – диаметр, r – радиус, π – это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.

Вывод

• Периметр – это мера длины, которая используется для измерения длины границы фигуры.
• Мы представили набор формул, который поможет вам эффективно решать задачи, связанные с нахождением периметра фигур в работе или образовательных целях.
• Для тех, кто хочет упростить процесс вычисления периметра, мы собрали топ популярных онлайн-калькуляторов.