Как найти дискриминант квадратного уравнения?

Решение квадратных уравнений – типовая задача для учеников 8 и более старших классов общеобразовательной школы. Причем она не относится к числу чисто теоретических, так как очень часто встречается на практике. Например, при расчете скорости движения, площадей и множества других параметров. Одним из распространенных способов решения квадратного уравнения выступает дискриминант. Рассмотрим более внимательно, что означает этот термин, а также как именно можно решать квадратные уравнения с помощью дискриминанта.

Квадратное уравнение и дискриминант: определение и математическое значение

Уравнением называют равенство, в котором содержится переменная. Его решение в общем случае означает вычисление значения этой переменной, которое называется корнем уравнения.

Квадратными считаются уравнения, имеющие следующий вид: ax² +bx + c = 0, где:

• х – это переменная, значение которой требуется найти;
• а, b и c – коэффициенты или действительные числа (причем «а» не должно равняться 0).

Левая часть уравнения называется квадратным трехчленом. Название термина легко понять простым визуальным изучением приведенной выше записи.

Решением квадратного уравнения становится поиск всех его корней или доказательство их отсутствия. Математика предоставляет в распоряжение школьников сразу несколько способов выполнения этой задачи. Включая:

• формулу дискриминанта (тема данной статьи);
• выделение так называемого полного квадрата;
• формулу теоремы Виета;
• разложение на множители квадратного трехчлена;
• графический и множество других.

Выбор оптимального способа зависит от уровня знаний ученика. Самыми распространенными считаются указанные в списке во втором и третьем пункте. Но они не являются темой данной статьи, поэтому далее рассматривается первый вариант решения квадратного уравнения.

Дискриминант представляет собой многочлен, который составляется из коэффициентов квадратного трехчлена. С его помощью определяется количество корней уравнения и значение каждого из них. Дискриминант обозначается буквой D. Его значение для типового квадратного уравнения определяется по следующей формуле: D = b2 – 4ac.

Как с помощью дискриминанта решить квадратное уравнение?

Последовательность действия для решения квадратных уравнений выглядит следующим образом:

1. Поиск значений трех коэффициентов (а, b и с).
2. Расчет дискриминанта по приведенной выше формуле.
3. Определение знака дискриминанта и количества корней квадратного уравнения с использованием следующих правил:
   1. если D=0, у уравнения один корень, который рассчитывается по формуле:
      
      
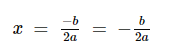
   2. если D>0, необходимо найти два корня, которые вычисляются следующим образом:
      
      
   3. если D<0, уравнение не имеет действительных корней.
4. Поиск корней.
5. Формулирование и запись ответа.

Примеры задач с квадратными уравнениями и их решения

Приведенное в предыдущем разделе статьи описание решения квадратного уравнения с помощью дискриминанта выглядит достаточно простым и понятным. Но в любом случае целесообразно закрепить изложенные знания на практике. Для чего имеет смысл привести несколько задач с примерами решений. Для краткости в тексте задачи приводится только само квадратное уравнение, корни которого требуется найти.

Задача №1. x² – 2x – 48 = 0.

Решение предусматривает последовательное выполнение действий в соответствии с описанной выше пошаговой инструкцией:

1. Определение значений коэффициентов: а = 1, b = -2, с = -48.
2. Расчет дискриминанта: D = (-2)² - 4*1*(-48) = 4+192 = 196.
3. D>0, поэтому уравнение имеет 2 корня.
4. Корни рассчитываются по следующим формулам:
   
   
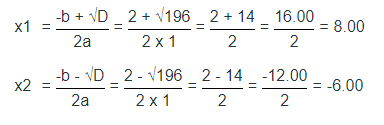
5. Ответ: 8 и -6.

Задача №2. 12х² + 8х + 10 = 0.

Решение выполняется в том же порядке и выглядит следующим образом:

1. Определение значений коэффициентов: a = 12, b = 8, c = 10.
2. Расчет дискриминанта: D = 8² – 4*12*10 = -416.
3. D<0, то есть у уравнения нет действительных решений.

Задача №3. 3х² + 12х + 12 = 0.

Решение задачи будет таким:

1. Определение значений коэффициентов: a = 3, b= 12, c= 12.
2. Расчет дискриминанта: D = 12² – 4*3*12 = 0.
3. D=0, поэтому у уравнения один корень.
4. Его расчет выглядит так:
   
   
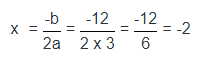
5. Ответ: -2.

Онлайн-калькуляторы

Сегодня школьникам и студентам при проведении различных математических расчетов помогают многочисленные онлайн-сервисы. Включая удобные и точные калькуляторы дискриминанта, позволяющие быстро и точно решить любое квадратное уравнение. В качестве примера можно привести следующие интернет-ресурсы:

• https://calc.by/math-calculators/quadratic-equations.html;
• https://discriminant-online.ru/;
• https://kalk.pro/math/raschet-diskriminanta/;
• https://math.semestr.ru/math/discriminant.php;
• https://ru.onlinemschool.com/math/assistance/equation/quadratic/.

Некоторые из них дают на выходе полное решение, часть – более простых – способны рассчитать дискриминант и определить количество корней. Выбор подходящей программы зависит от задач, стоящих перед учащимся, и имеющихся у него предпочтений.

FAQ

Что понимается под квадратным уравнением?

Это широко распространенное уравнение вида: ax² +bx + c = 0.

Что такое дискриминант?

Расчетный показатель, вычисление которого предусматривает использование коэффициентов из квадратного уравнения.

Как с помощью дискриминанта решить квадратное уравнение?

Значение дискриминанта показывает количество корней уравнения (один, если D=0, или два, если D> 0) или доказывает их отсутствие (если D<0). Значение корней вычисляется по достаточно сложным формулам, приведенным в статье.

Вывод

1. Квадратные уравнения представляют собой типовую задачу, которая актуальная для школьников, начиная с 8 класса.
2. Одним из эффективных и доступных способов ее решения выступает дискриминант, представляющий собой расчетный показатель, полученный по специальной формуле с использованием коэффициентов из квадратного уравнения.
3. Быстрее и проще всего решить квадратное уравнение с помощью дискриминанта при одновременном задействовании онлайн-калькулятора. Значительная часть подобных ресурсов доступна в бесплатном формате и не требует даже регистрации на сайте.