График линейной функции

График линейной функции – это удобный инструмент для визуализации и анализа зависимостей между двумя переменными. Понимание его определения и возможностей может быть полезным при изучении и применении математики в различных областях знаний.

В этой статье мы узнаем свойства графика линейной функции, разберем формулы вычисления и способы построения функции.

Основные понятия

Функция – это математическая связь между двумя переменными, где каждому значению одной переменной соответствует только одно значение другой переменной. Задать функцию можно несколькими способами:

• графическим, наглядно на рисунке;
• словесно;
• аналитически, с помощью формул;
• в таблице.

Линейная функция описывает прямую линию на графике. Она имеет следующий вид:

y = m * x + b, где, m – наклон прямой (коэффициент наклона), b – точка пересечения с осью ординат (y-ось);

Если известно конкретное значение х, можно вычислить соответствующее значение у.

График линейной функции

График линейной функции – это двумерная визуализация математической функции, которая описывает зависимость между двумя переменными. Линейная функция является простейшим видом функции, где график представляет собой прямую линию.

График линейной функции имеет множество практических применений в различных сферах, таких как экономика, физика и инженерия. С его помощью можно предсказывать зависимости между переменными, анализировать данные и многое другое.

Для определения графика линейной функции необходимо знать две ключевые характеристики: коэффициент наклона и точку пересечения с осью ординат (y-ось):

• Коэффициент наклона – определяет, насколько быстро меняется значение функции по отношению к изменению значения независимой переменной. Обозначается как «k». Если значение k положительное, график линейной функции будет направлен вверх справа налево. Чем больше значение k, тем круче будет наклон графика. Если значение k отрицательное, график будет направлен вниз слева направо.
• Точка пересечения с осью ординат – определяет значение функции при нулевом значении независимой переменной или точку, где график пересекает ось ординат. Обозначается как «b». Коэффициент k определяется как угол наклона прямой к положительному направлению оси OX. Он считается против часовой стрелки. Также, его можно определить как длину отрезка, который отсекает прямая по оси OY, считая от начала координат.

Необходимые значения вычисляются по формуле:

y = k * x + b, где х – независимая переменная, и коэффициенты k, b. При этом k – угловой коэффициент, b – свободный коэффициент.

Если k > 0, то этот угол острый, если k < 0 — тупой, если k = 0, то прямая совпадает с осью OX.

Зная коэффициенты наклона и точку пересечения с осью ординат, можно построить график линейной функции. Для этого проводим оси координат, откладываем точку пересечения с осью ординат, а дальше, используя значение k, строим прямую линию, проходящую через эту точку.

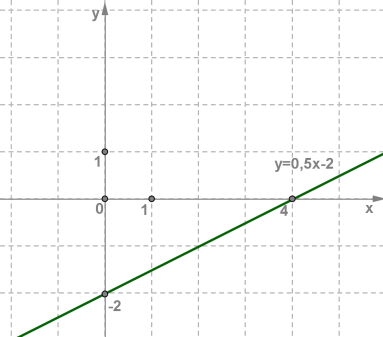
Пример графика линейной функции

Попробуем определить значения коэффициентов k и b:

Частные случаи линейной функции

Существует два частных случая линейной функции в зависимости от значений коэффициентов:

1. При b = 0, формула примет вид y = k * x. Такая функция называется прямой пропорциональностью. Его график – это прямая, которая проходит через начало координат. Постройте графики таких функций следующим образом:
   
   
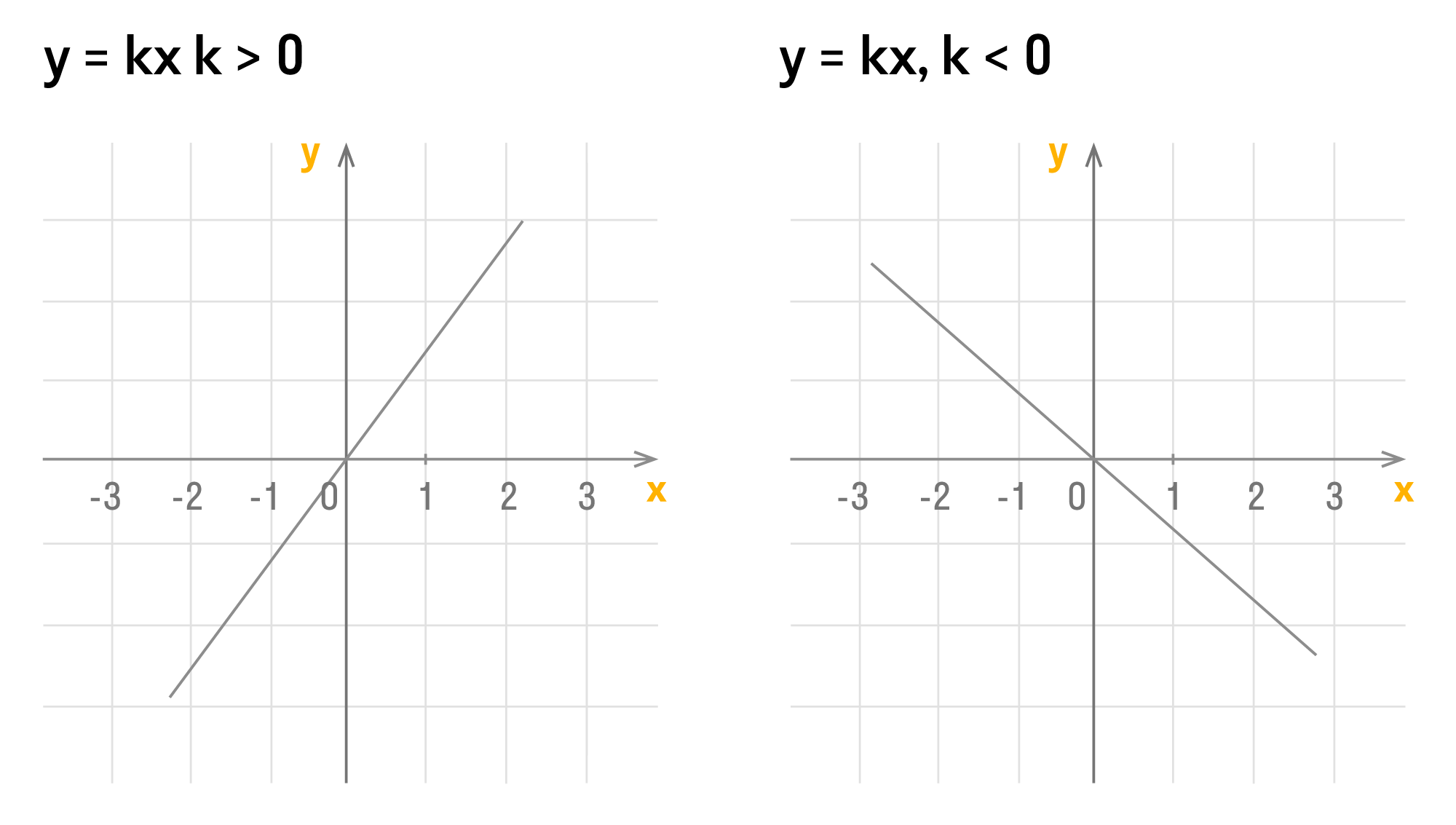
2. При k = 0, уравнение примет вид y = b. Его график – это прямая, параллельная оси OX и проходящая через точку (0; b). Пример такого графика:
   
   

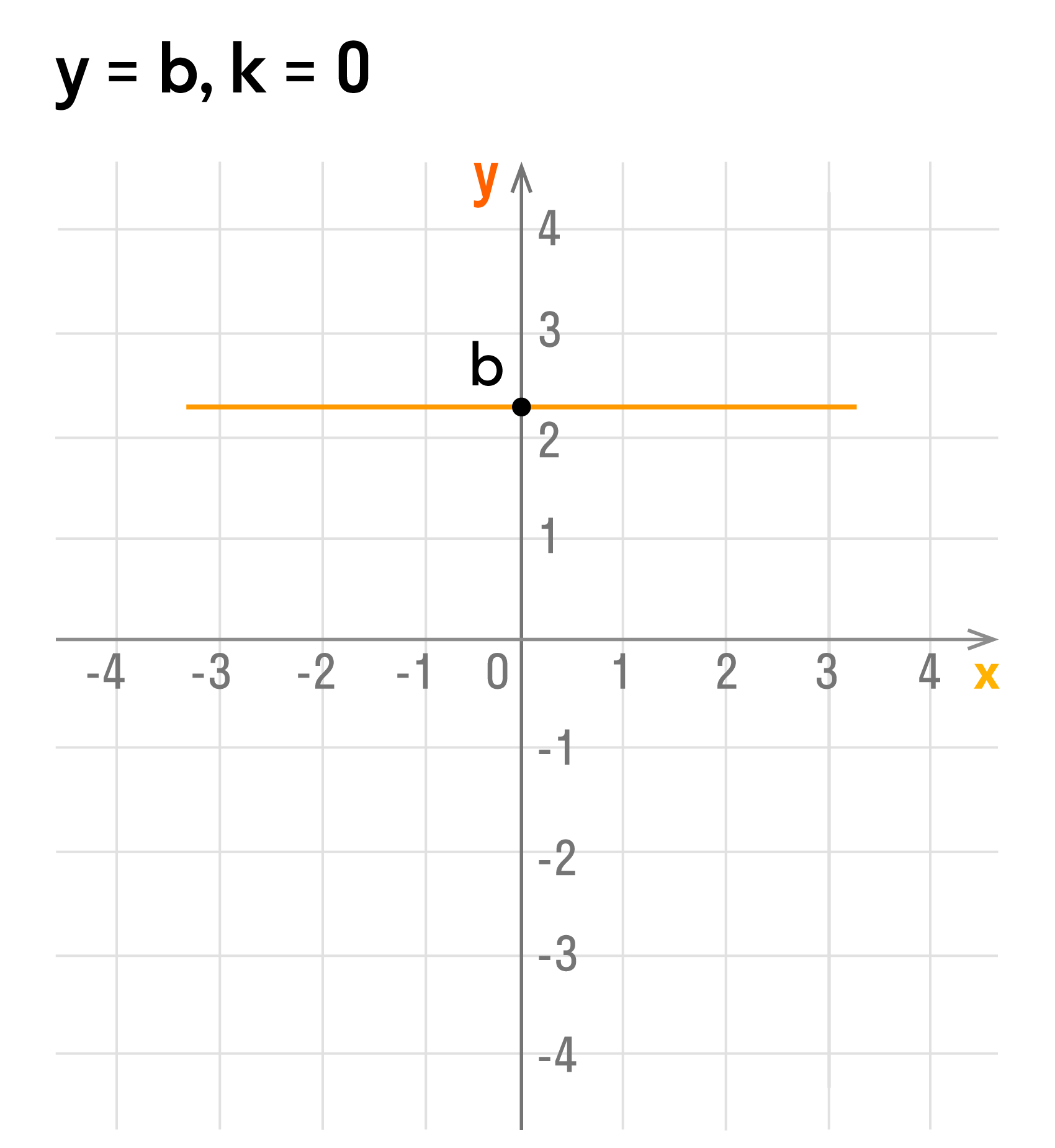
Свойства линейной функции

К свойствам линейной функции можно отнести следующие:

• График линей функции изображает прямую линию.
• Для построения прямой на координатной плоскости, необходимо знать значение коэффициентов k и b.
• Линейная функция не обладает свойством периодичности.
• У функции нет наибольшего или наименьшего значения.
• Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
• b ≠ 0, k = 0, значит, уравнения y = b – четная;
• b = 0, k ≠ 0, значит, уравнения y = kx – нечетная;
• b ≠ 0, k ≠ 0, значит, уравнения y = kx + b – функция общего вида;
• b = 0, k = 0, значит, уравнения y = 0 – как четная, так и нечетная функция.
• Линейные функции имеют постоянный наклон на всей области определения.
• Функция возрастает монотонно при k > 0 и монотонно убывает при k < 0.
• Если, k > 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).
• Если, k < 0 функция принимает отрицательные значения на промежутке (−b/k; +∞) и положительные значения на промежутке (−∞; −b/k).
• Если b имеет положительное значение, то прямая пересекает ось ординат выше начала координат, а если отрицательное, то ниже.
• Ее график пересекает ось абсцисс OX (в точке b/k; 0) и ось ординат OY (в точке 0; b).
• Ноль функции – это x = −b/k
• Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
• Если b ≠ 0 и k = 0, то функция y = b не обращается в ноль ни при каких значениях переменной х.
• Линейная функция обладает свойством аддитивности: f(x + y) = f(x) + f(y).
• Линейная функция используется для решения систем линейных уравнений и неравенств, а также для нахождения точек пересечения графиков функций.

Как построить линейную функцию

Чтобы построить график линейной функции вида у = k * x + b необходимо иметь значения двух точек и найти значение x.

Например, для построения графика функции y = 1/3x + 2, можно взять х = 0 и х = 3. Исходя из этих данных, мы выясним, что ординаты этих точек будут равны у = 2 и у = 3. Таким образом мы получим точки А (0; 2) и В (3; 3). После их соединения получается такой график:

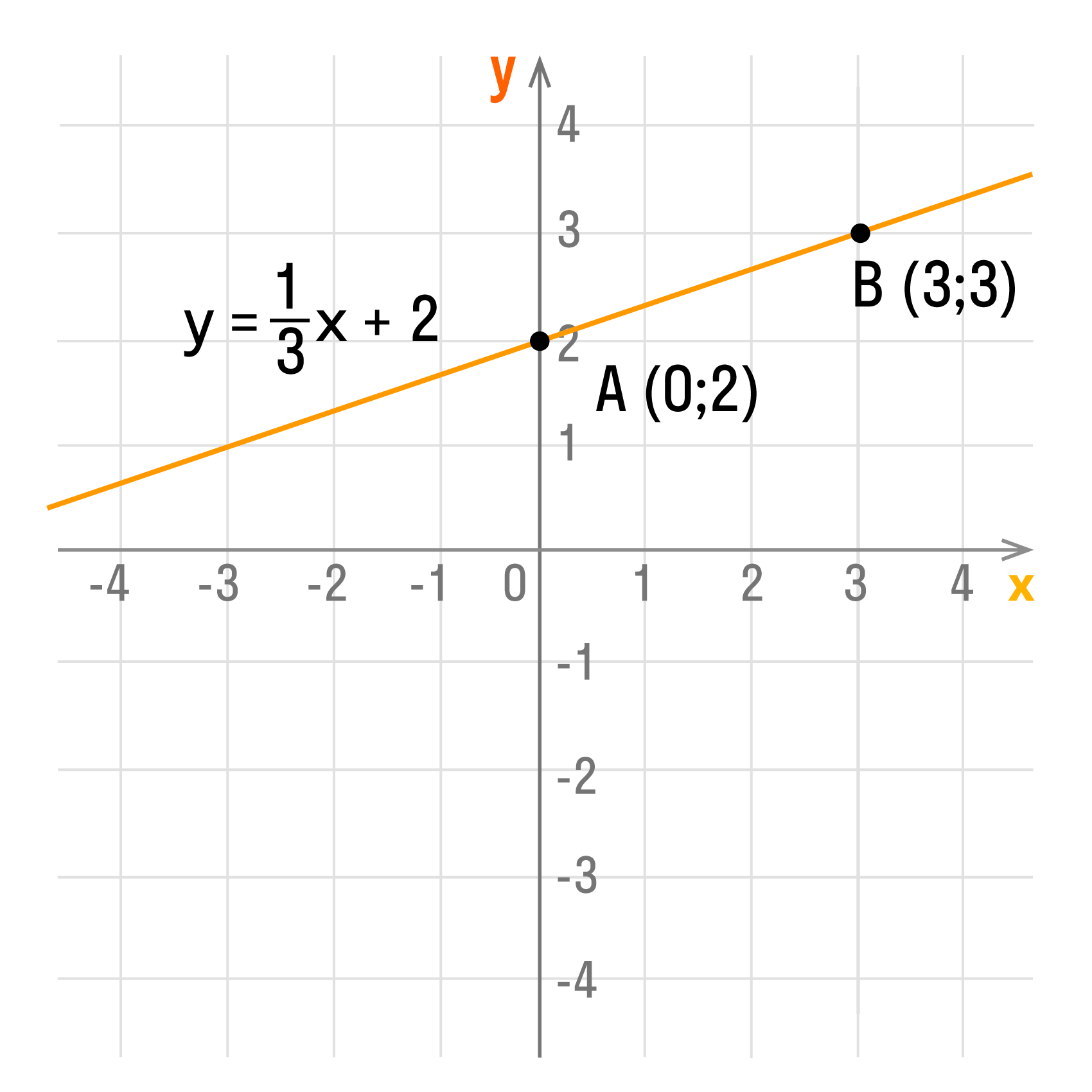
Примеры решения задач

Разберем несколько задач, в которых необходима формула линейной функции.

Пример 1.

Задание: Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

Решение:

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставив координаты точки в уравнение, получим равенство и вычисляем значение по коэффициенту b:

2 = -4(-3) + b

b = -10

Следовательно, необходимо построить график функции y = -4x – 10.

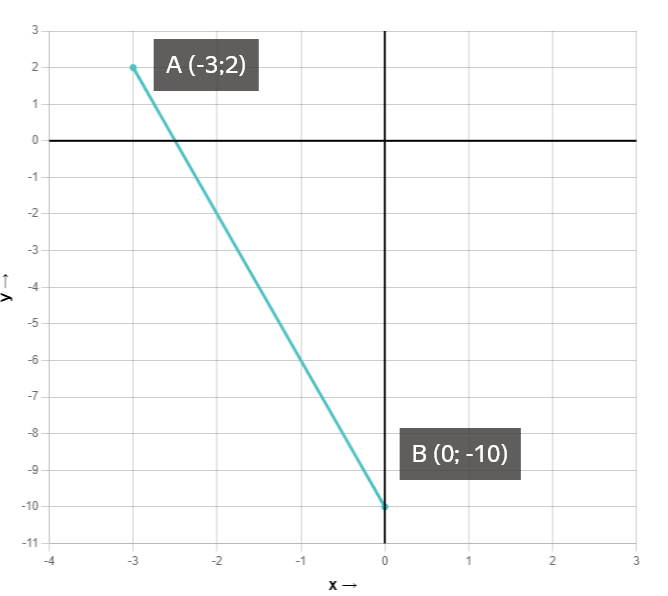
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой по графику линейной функции:

Пример 2.

Задание: Написать уравнение прямой, которая проходит через точки A (2; 3); B (4; 6).

Решение:

Координаты точек подходят под уравнение y = kx + b, следовательно, подставляем их данные и получаем систему линейных уравнений:

При вычитании первого уравнения из второго, мы получим k = 3.

Подставим k = 3 в первое уравнение и получим: 1 = 3 + b, из чего делаем вывод, что b = -2.

Таким образом, уравнение прямой будет иметь следующий вид:

y = 3x – 2.

FAQ

Можно ли упростить процесс построения графиков функций?

В интернете есть множество сайтов, на которых вы можете построить графики линейных функций. Вот несколько самых популярных:

• Desmos. Здесь можно строить графики линейных функций по различных формулам, просто подставляя необходимые значения коэффициентов.
• Buildingclub. Данный сайт позволяет строить графики линейных функций по координатам точек.
• Yotx. Сервис предназначен для онлайн построения графиков функций (обычных и параметрических) и графиков по точкам (по значениям), а также графиков функций в полярной системе координат.

Можно ли научиться строить графики самостоятельно?

Да, при должном внимании вы сможете изучить тему самостоятельно, ведь она не сложная и подробно описана в нашей статье, а также на многих форумах и в видеоуроках.

Вывод

• Линейные функции позволяют анализировать и описывать линейные зависимости между переменными.
• Они обладают простыми алгебраическими свойствами, что делает их легко изучаемыми и применимыми в различных математических и научных областях.
• График функции позволяет наглядно представить зависимость между двумя переменными и сделать выводы о её свойствах и значениях при различных условиях.
• В этой статье мы рассмотрели все свойства линейных функций и решили несколько задач по теме.
• Для тех, кто не хочет строить графики от руки, мы подобрали топ популярных онлайн-сервисов, которые облегчат это дело.