Длина вектора
Понятие вектор встречается в физике, алгебре и геометрии. Он помогает решать задачи различной сложности и тематики.
В этой статье мы расскажем, что такое вектор, как найти его длину, разберем несколько примеров и посмотрим обзор на онлайн-калькуляторы.
Векторы – что такое
Вектор – это математический объект, который характеризуется не только величиной, но и направлением. Он определяется как совокупность чисел, обычно представленных в виде упорядоченной последовательности или столбца. Каждое из этих чисел представляет собой компоненту вектора в определенном направлении.
Обозначение направленного отрезка – 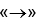 , например
, например 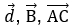 и т.д. Это означает, что вектор можно назвать как одной буквой, так и двумя точками, которые будут являться началом и концом:
и т.д. Это означает, что вектор можно назвать как одной буквой, так и двумя точками, которые будут являться началом и концом:
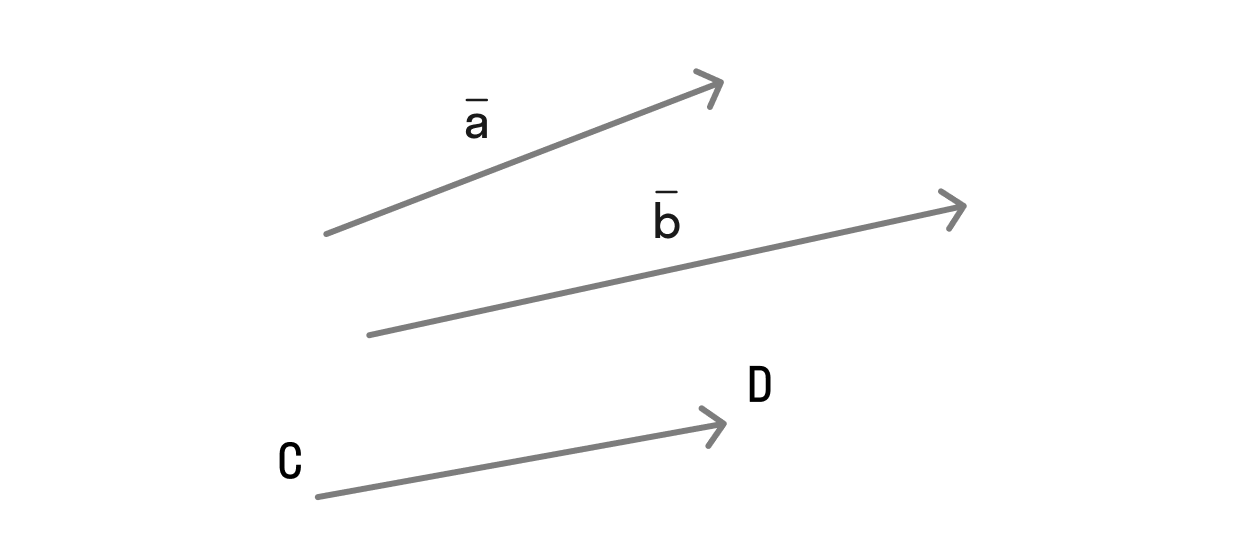
Какими бывают
Вектора бывают следующих видов:
- Нулевой вектор – это вектор, который не имеет определенного направления и не может быть коллинеарным или неколлинеарным ни с каким другим вектором. Символом нулевых вектора является
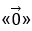 .
. - Коллинеарные векторы – это векторы, которые лежат на одной прямой или параллельны друг другу. Они имеют одно и то же направление или противоположное направление, но различаются по своей длине.
- Неколлинеарные векторы – это векторы, которые не лежат на одной прямой и не параллельны друг другу. Они могут иметь различные направления и различные длины.
- Сонаправленные векторы – это векторы, которые могут быть коллинеарными или неколлинеарными, но имеют общее направление.
- Противоположно направленные векторы – это векторы, которые имеют противоположное направление друг от друга. Они всегда коллинеарны и могут быть выражены как масштабирование друг друга с отрицательным масштабным множителем.
Все эти понятия объединяет то, что у каждого вектора есть длина. Разберемся, что это подробнее.
Длина вектора
Длина вектора представляет собой меру величины и направления вектора, и позволяет нам определить его абсолютное значение. Иногда длину вектора называют модулем и выглядит это так 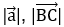 и т.д. Исходя из того, что длину вектора называют модулем, можно понять – длина всегда будет положительной, не важно в какую сторону направлен вектор.
и т.д. Исходя из того, что длину вектора называют модулем, можно понять – длина всегда будет положительной, не важно в какую сторону направлен вектор.
Длина нулевого вектора всегда будет равна 0.
Понятие длины вектора имеет множество практических применений:
- Оно позволяет нам измерить физическую величину, такую как скорость, силу или напряжение. Например, мы можем определить, насколько быстро движется объект в определенном направлении.
- В геометрии используя длины векторов можно определить угол между ними и их скалярное произведение.
- Длина вектора играет важную роль в определении различных метрик и коэффициентов, используемых в математическом анализе и статистике. Так, длина вектора может быть использована для измерения сходства или различия между двумя наборами данных.
- Также она позволяет определить единичный вектор, то есть вектор с длиной равной единице. Единичные векторы широко применяются в различных областях, таких как компьютерная графика, робототехника и криптография.
Как найти длину вектора по координатам
Чтобы найти длину вектора по координатам необходимо воспользоваться прямоугольной системой координат. Разберем решение подробнее на примере.
Допустим, у нас есть вектор 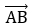 (х;у), который выходит из точки А с координатами (0;0).
(х;у), который выходит из точки А с координатами (0;0).
Такой вектор можно считать радиус-вектором для двух других векторов (АВ1 И АА1).
Примем обозначения для длин векторов: |АВ1| = у, |АА1| = х.
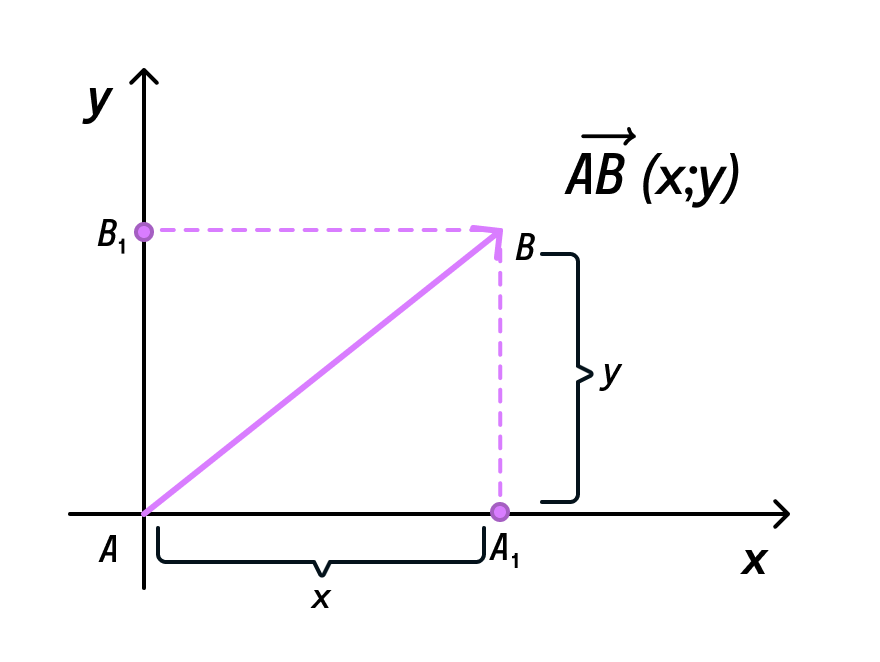
Получаем два прямоугольных треугольника АА1В и АВВ1 с общей гипотенузой АВ. Длину гипотенузы можно найти по теореме Пифагора:
АВ2 = АА12 + АВ2 = х2 + у2
Из данной формулы получаем, что:
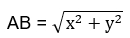
Если объяснять словами, то для того, чтобы найти длину вектора 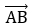 необходимо сложить сумму квадратов его координат и взять их в квадратный корень.
необходимо сложить сумму квадратов его координат и взять их в квадратный корень.
Итоговая формула вычисления длины вектора по координатам будет выглядеть так:
Для трехмерного пространства формула поиска длины вектора 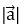 = (ах, ау, аz) будет выглядеть так:
= (ах, ау, аz) будет выглядеть так:
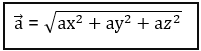
Рассмотрим, как работают эти формулы на примерах.
Пример 1
Необходимо найти модуль вектора 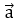 = (-5; 8).
= (-5; 8).
Решение:
Подставим данные в формулу вычисления длины вектора:
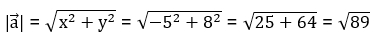
Ответ: длина вектора равна 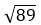
Пример 2
На каком расстоянии от начала координат находится точка А (4; 1)?
Решение:
Вектор 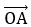 является радиус-вектором, следовательно его координаты совпадают с координатами точки А, что означает
является радиус-вектором, следовательно его координаты совпадают с координатами точки А, что означает 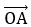 (4;1). Подставим эти данные в формулу, чтобы вычислить длину:
(4;1). Подставим эти данные в формулу, чтобы вычислить длину:
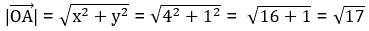
Ответ: точка А находится на расстоянии в 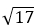 .
.
Как найти длину вектора по двум точкам
Бывают случаи, когда в задаче нам не дают координаты вектора. В таких случаях, длину вектора можно найти по координатам двух точек – начала и конца.
Координаты вектора 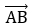 в точке А (ха; уа), в точке В (хв; ув), следовательно вектор
в точке А (ха; уа), в точке В (хв; ув), следовательно вектор 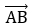 имеет координаты (хв – ха; ув – уа). Таким образом, формулы нахождения длины вектора по двум точкам будет выглядеть так:
имеет координаты (хв – ха; ув – уа). Таким образом, формулы нахождения длины вектора по двум точкам будет выглядеть так:
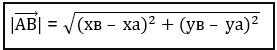
Разберем данную формулу на примере:
Необходимо найти длину вектор 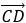 , точки имеют координаты С (4;6), D (-2; 0).
, точки имеют координаты С (4;6), D (-2; 0).
Решение:
Подставим данные в формулу:
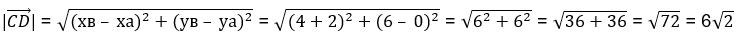
Ответ: длина вектора 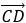 равна
равна 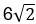 .
.
Как найти длину вектора при помощи теоремы косинусов
Некоторые задачи по поиску длины вектора можно решить с помощью теоремы косинусов. Звучит она так:
- Квадрат стороны треугольника состоит из равного сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
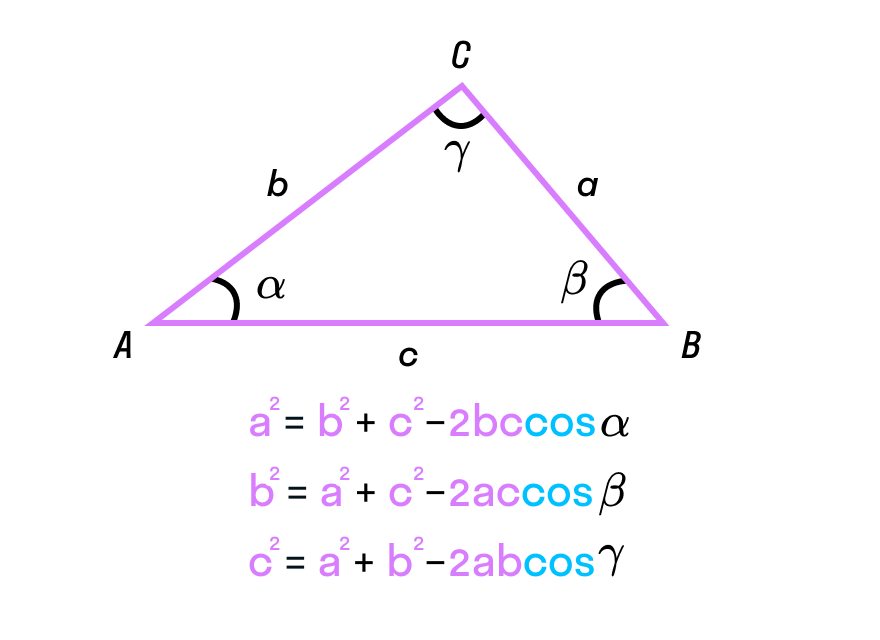
Формулы в этом случае, будут выглядеть так:
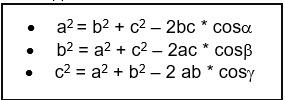
Решим пример, чтобы точнее понять, как определять длину вектора через теорему косинусов.
Пример:
Дано три вектора: 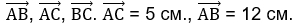 , угол между ними равен π/3.
, угол между ними равен π/3.
Необходимо найти длину вектора 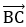 .
.
Решение:
Отразим данные, которые нам даны на рисунке, для наглядного понимания:
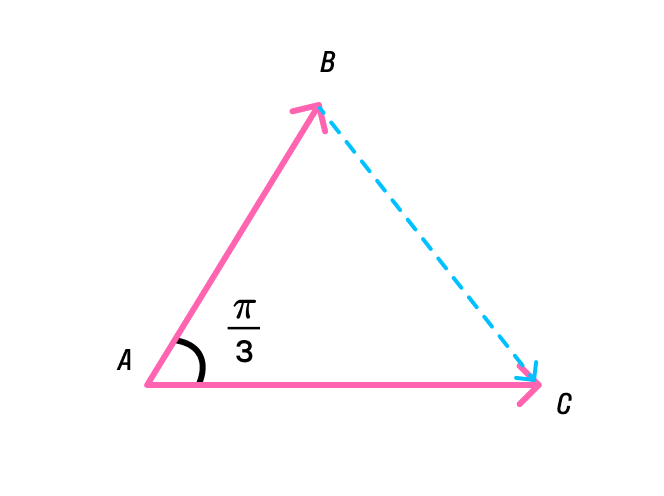
Для начала найдите квадрат длины вектора. Чтобы это сделать, подставим известные нам данные в теорему косинусов:

Ответ: длина вектора 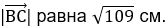
Онлайн-калькуляторы – обзор
Для тех, кто хочет быстрее и проще вычислять длину вектора, мы подобрали Топ-3 онлайн-калькулятора, которые бесплатно помогут выполнить задачу:
- OnlineMSchool – онлайн калькулятор позволит очень просто найти длину вектора для плоских и пространственных задач. Воспользовавшись им, вы получите детальное решение задачи, которое позволит понять алгоритм решения на вычисление модуля вектора и закрепить пройденный материал.
- Калькулятор – сервис поможет найти длину (модуль) двумерного или трехмерного вектора, заданного в виде координат либо точек или используя две стороны прямоугольника.
- AllCalc – при помощи калькулятора можно упростить процесс расчетов. Для этого потребуется выбрать тип пространства и ввести в соответствующие поля значения X и Y (Z – в трехмерной системе).
FAQ
Чему равна длина единичного вектора?
Единичным вектором называется вектор, длина которого равна единице.
Для нахождения длины единичного вектора необходимо применить формулу вычисления нормы вектора. Например, в трехмерном пространстве длина единичных векторов, заданных координатами (x, y, z), вычисляется следующим образом:
(x2 + y2 + z2) * (1/2) = 1.
Можно ли освоить данную тему без учителя?
Да, вы можете самостоятельно научиться вычислять длину вектора. В нашей статье есть все необходимые формулы и пояснения, которые помогут вам в этом вопросе.
Вывод
- Вектор указывает на конкретное направление в пространстве.
- Векторы могут быть представлены в различных формах, включая координатную, геометрическую и алгебраическую формы.
- Длина вектора равна квадратному корню из суммы квадратов координат.
- В нашей статье представлены все формулы для вычисления длины вектора с примерными задачами.
- Упростить процесс вычисления можно, воспользовавшись специальными онлайн-калькуляторами, которые мы подобрали для вас.

