Длина окружности

Из уроков математики каждый школьник знает, что у каждой фигуры есть периметр, который представляет собой сумму длин всех сторон. Найти это значение для квадрата, треугольника и т. д. просто. Но, как быть с окружностью, ведь у нее нет сторон? Для этой фигуры есть свои формулы, которые и рассмотрим ниже.

Длина окружности

Таким понятием обозначают длину границы у круга. В формулах длину обозначают буквами L или С. Далее для обозначения длины окружности, будем использовать латинскую букву С.

Для начала стоит познакомиться с полезной и интересной информацией:

1. Над расчетами длины окружности, люди работали с древних времен. Но, тогда они определяли этот показатель с погрешностью. Та формула, которой мы пользуемся сегодня, была выведена древнегреческим математиком Архимедом в III веке до нашей эры.
2. При вычислении длины окружности, потребуется число π. Эта важная математическая постоянная, значение которой равно около 3,14.
3. Длина окружности может обозначаться двумя способами – латинскими буквами L и С. Последний вариант используют чаще.
4. Существует много способов расчета длины окружности. Используют обычно тот вариант, в котором у нас известно большинство данных либо же их легко найти.

Как найти длину окружности зная диаметр

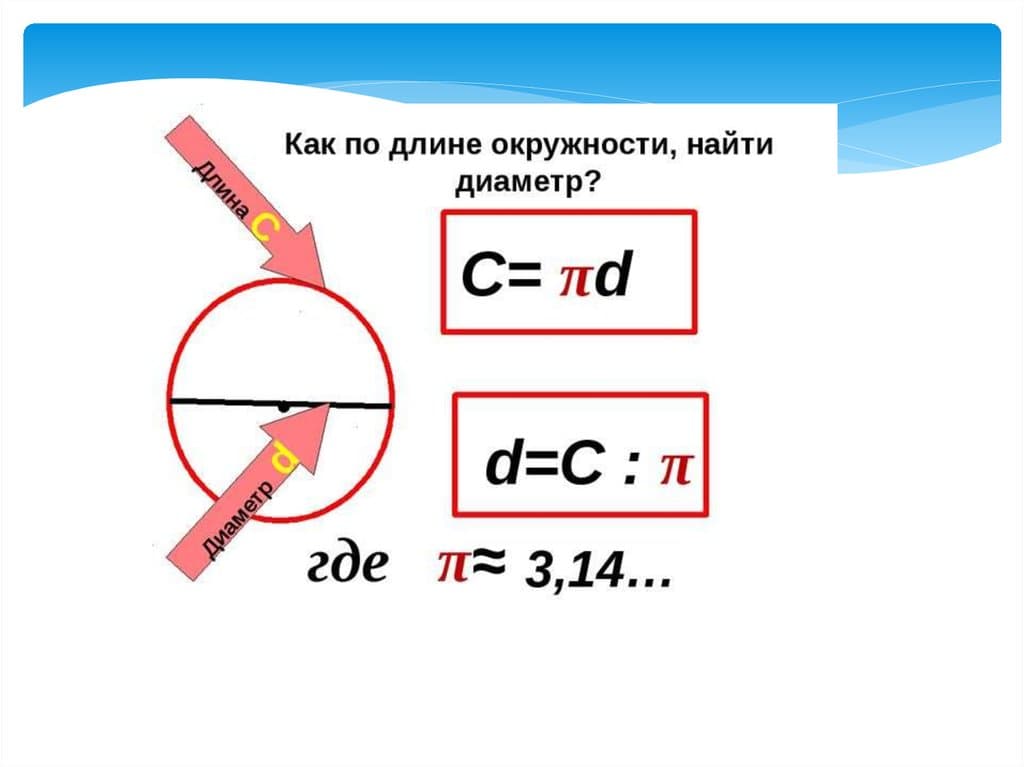
Отрезок, соединяющий 2 разные точки, расположенные на окружности, называется хорда. Хорда, проходящая через центр, называется диаметром. Ее длина максимальная. Зная величину диаметра, можно рассчитать длину окружности. Формула выглядит следующим образом:

С=π*d, где

d – диаметр окружности;

π=3,14 – математическая константа.

Как найти длину окружности зная радиус

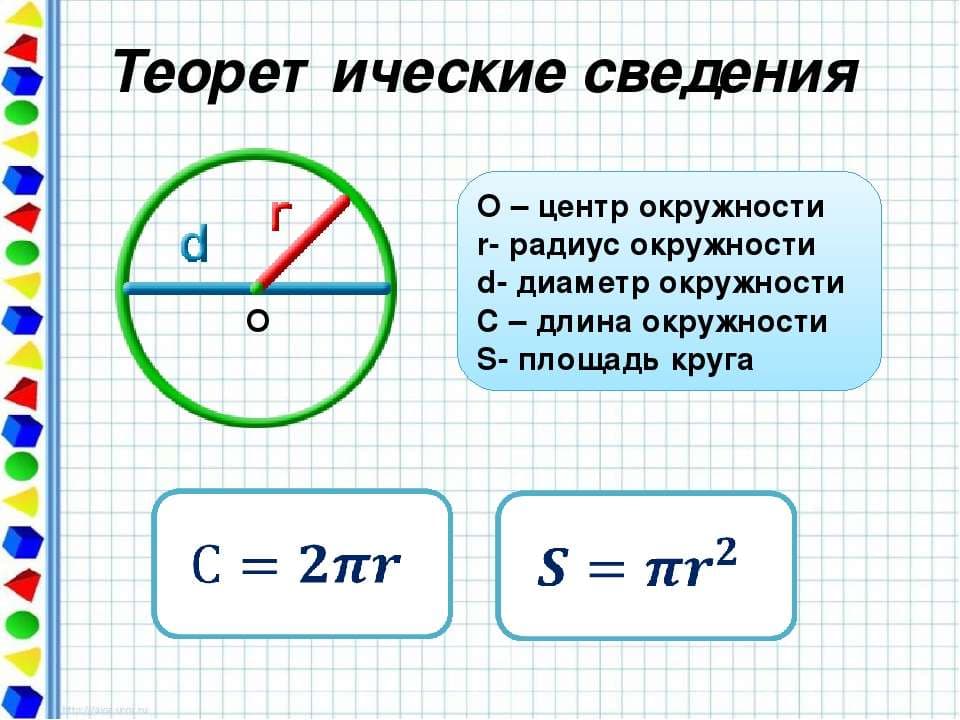
Отрезок, соединяющий точку на окружности с ее центром. Зная радиус, найти длину окружности можно с использованием такой формулы:

С=2πr, где

r – радиус окружности;

π=3,14 – математическая константа.

Перечисленные формулы, учитывающие радиус и диаметр окружности при расчете ее длины, являются основными. Но, кроме них есть и другие варианты нахождения длины окружности, с учетом свойств геометрических фигур.

Как найти длину окружности, зная площадь круга

Если в задании дана площадь круга, можно использовать формулу, чтобы найти длину ее окружности. Формула выглядит следующим образом:

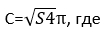
S – известная площадь круга;

π=3,14 – математическая константа.

Как найти длину окружности, зная величину диагонали вписанного прямоугольника

Если по условию задачи дано, что в окружность вписан прямоугольник, то для расчета ее длины, можно использовать следующую формулу:

C= π*d, где

d – диагональ прямоугольника;

π=3,14 – математическая константа.

Как найти длину окружности, зная длину стороны описанного квадрата

Если по условию задачи имеется вписанная внутрь квадрата с известной стороной окружность, то для расчета ее длины, используют формулу:

С=π*а, где

а – длина стороны квадрата;

π=3,14 – математическая константа.

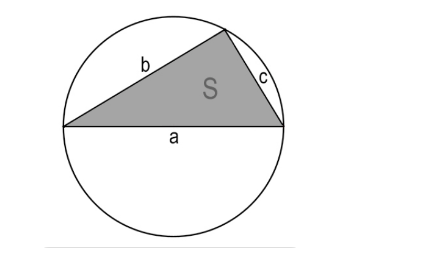
Как рассчитать длину окружности, зная площадь и стороны вписанного в нее треугольника

Если по условию известны длины сторон треугольника, вписанного в окружность и его площадь, то для расчета длины окружности можно использовать формулу:

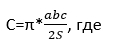
а – длина одной стороны треугольника;

b – длина другой стороны треугольника;

с- длина третьей стороны треугольника;

S – площадь треугольника;

π=3,14 – математическая константа.

Как рассчитать длину окружности, зная полупериметр и площадь описанного треугольника

Рассчитать длину окружности вписанной в треугольник получится, если в условии известны: полупериметр и площадь треугольника.

Из уроков математики известно, что периметром называют сумму длин всех сторон фигуры. Соответственно полупериметр – это половина периметра. Чтобы найти это значение, необходимо рассчитать, чему равен периметр треугольника и полученное число разделить на 2. После этого получится рассчитать длину окружности по формуле:

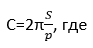
р – полупериметр треугольника;

S – площадь треугольника;

π=3,14 – математическая константа.

Как рассчитать длину окружности, если известны стороны многоугольника, вписанного в окружность

Чтобы рассчитать, какова длина окружности в таком примере, нужно посчитать количество сторон вписанного многоугольника и знать длину каждой из них. Рассмотрим пример, в котором мы имеем правильный многоугольник, то есть длины каждой из его сторон одинаковые. Исходя из этого, используем следующую формулу:

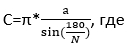
N – число сторон у многоугольника;

а – длина одной стороны многоугольника;

π=3,14 – математическая константа.

Онлайн-калькуляторы – обзор сервисов

В интернете представлено большое количество сервисов, с помощью которых можно легко рассчитать длину любой окружности. Самыми популярными из них являются следующие онлайн-калькуляторы:

1. Калькулятор окружности. На сервисе нужно ввести известные значения и система автоматически рассчитает длину окружности.
2. Skysmart. Сервис позволяет рассчитать длину окружности несколькими способами, исходя из входных данных.
3. Calculatus.ru. Здесь можно рассчитать длину любой окружности, исходя из известных диаметра, радиуса, площади круга.
4. Poschitat.online. Зная радиус, окружность или площадь круга, система способна рассчитать длину его окружности.
5. OnlineMSchool. Воспользовавшись сервисом, можно не только получить ответ, но и детальное решение примера. Это даст возможность самостоятельно разобраться с алгоритмом решения.

Разберем примеры – задачи и решение

Чтобы закрепить материал, стоит решить несколько простых примеров:

Задача 1:

Необходимо рассчитать длину окружности, если известно, что ее диаметр равен 10 см.

Решение. Зная диаметр окружности, можно воспользоваться формулой С=π*d. Подставив сюда известные данные, получаем С=3,14*10=31,4 см.

Задача 2:

Необходимо рассчитать длину окружности, если известно, что в нее вписан правильный треугольник, сторона которого равна 4 √3 см.

Решение. Для начала находим радиус круга.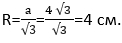

Узнав радиус окружности, мы можем рассчитать ее длину по формуле С=2πr.

С=2*3,14*4=25,12 см.

Задача 3:

Необходимо рассчитать длину окружности, если известно, что площадь круга равна 20 см.

Решение. Для расчета радиуса окружности используем формулу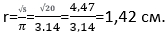

FAQ

Можно ли рассчитать длину окружности, зная только одну величину (радиус, диаметр или площадь круга)?

Да, есть формулы расчета длины окружности, в которой используется только один из перечисленных компонентов.

Почему число π не «ровное» число?

Π – представляет собой отношение длины окружности к ее диаметру. Проведя математические вычисления, у нас получается иррациональное число, так как его значение нельзя представить обычной дробью 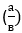, где а и в - целые, натуральные числа. Поэтому его десятичное представление не периодическое, так как никогда не заканчивается.

Вывод

Найти длину любой окружности не сложно, зная несколько простых формул, где ее обозначают буквами L или С. Чтобы проверить свои расчеты, можно воспользоваться онлайн-калькулятором.