Десятичные дроби

Десятичные дроби намного более активно используются в повседневной жизни, они более удобны для записи на компьютерах, проведения разного рода действий. Поговорим, о том, как найти десятичную дробь, чем она отличается от обыкновенной, расскажем про свойства десятичных дробей, преобразования и решим несколько примеров для закрепления материалов.

Понятие десятичной дроби – что это

Чтобы понять, что такое десятичные дроби, сначала стоит поговорить об обыкновенных. В обыкновенной дроби над чертой пишется делимое, которое становится числителем, а под чертой – знаменатель-делитель, а сама черта указывает на деление: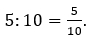 

В десятичной же дроби знаменатель всегда равен 10, 100, …. 1 000 000 и т.д. По сути, десятичная дробь указывает на то, что будет, если поделить числитель на знаменатель. Для записи десятичной дроби используется запятая, которая отделяет целую часть от дроби, например, 0,8; 5,356 и т.д.

Любую десятичную дробь можно представить в виде обыкновенной:

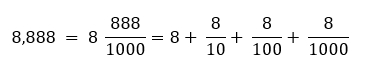
Существуют конечные десятичные дроби – те, которые имеют точно определенное количество цифр после запятой.

Бесконечной десятичной дробью называется десятичная дробь, в которой количество цифр является бесконечным. Для удобства математики округляют эти цифры до 1-3 после запятой.

Свойства десятичных дробей

Главным свойством десятичных дробей является то, что, если к ней справа приписать любое количество нулей – ее величина не поменяется. Если в вашей десятичной дроби большое количество нулей, то их можно отбросить. Например:

• 0,53000000 = 0,53
• 878,991900000000000 = 878,9919.

Кроме того, у десятичных дробей есть свойства, связанные с обыкновенными дробями:

• Целая часть десятичной дроби = целой части смешанной. Если числитель меньше знаменателя, то целая часть = 0.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же обыкновенной дроби.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. Значит, что если после запятой 1 цифра, значит делителем было число 10, если после запятой 10 цифр, то делителем было число 10 000 000 000.

Как записать десятичную дробь

Чтобы записать десятичную дробь, необходимо сначала написать целую часть, потом поставить запятую и в конце – записать числитель дробной части. Например, при переводе обыкновенной дроби 25/10 в десятичную, необходимо действовать по следующему алгоритму:

• Выделяем целую часть – 2
• Ставим запятую – 2,
• Указываем дробную часть – 2,5.

Как читать десятичную дробь

Для того, чтобы вас правильно понимали окружающие, когда речь заходит о десятичных дробях, сначала произносятся целые с добавлением слова «целых», а после – дробная часть с добавлением названия разряда, который зависит от количества цифр после запятой:

Дальше разряды формируются по тому же принципу.

Преобразование десятичных дробей

Преобразование десятичных дробей может стать серьезной задачей, так как десятичные дроби могут становиться другими носителями информации.

Как перевести десятичную дробь в обыкновенную?

Для того, чтобы перевести десятичную дробь в обыкновенную, необходимо действовать по простому алгоритму. Рассмотрим его на примере десятичной дроби 23,23:

1. Перепишем исходную дробь в новый вид: в числитель поставим десятичную дробь, а в знаменатель 1. Получится: 23,23/1.
2. Умножим числитель и знаменатель на столько раз, чтобы в числителе исчезла запятая. После каждого умножения запятая в числителе сдвигается право на один знак, а у знаменателя добавляются нули: 22,23/1=232,3/10=2323/100.
3. После этого можно сократить полученный результат. В нашем примере сокращение не требуется, но если бы у нас получилось, например, 45/100, то можно сократить дробь на 5 и получить 9/20.

Не стоит забывать про минус в ответе. Если изначальное число было отрицательным, то и после перевода обыкновенная дробь должна быть отрицательной.

Перевод десятичной дроби в проценты

Десятичная дробь напрямую связана с процентами. Дело в том, что 1% – 1/100 часть любого числа. Например, для 1% от 1 = 1/100 = 0,01.

Для перевода в проценты десятичную дробь, нужно просто убрать знак % и разделить число на 100, как в примере выше.

Для того, чтобы перевести десятичную дробь в проценты, наоборот, ее нужно умножить на сто и добавить знак процентов:

0,23 = 0,23*100% = 23%.

Это можно использовать для выражения обыкновенных дробей в процентах. Для этого сначала переводим обыкновенные дроби в десятичную, а после используем правило выше:

3/5 = 0,6

0,6*100%= 60%.

Действия с десятичными дробями

Десятичные дроби используются для тех же действий, что и любые другие числа:

• умножение;
• деление;
• вычитание;
• сложение.

При этом действия с ними можно совершать как с использованием натуральных чисел, так и отрицательных, обыкновенных дробей. Освоить особенности выполнения действий с десятичными дробями лучше на примерах с решениями и ответами.

Задачи – примеры и решение

Задача 1. Разделить 4,8 на 3/5

Для того, чтобы решить эту задачу, переведем 4,8 в обыкновенную дробь: 4,8=4,8/1=48/10.

Разделим дробь по правилам:

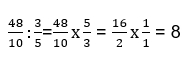
Задача 2. Умножить 4,8 на 3/5 и представить результат в виде десятичной дроби

Для того, чтобы решить эту задачу, переведем 4,8 в обыкновенную дробь: 4,8=4,8/1=48/10.

Умножим дроби по правилам:

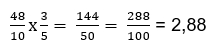
Задача 3. Перевести десятичную дробь 0,27 в проценты.

Для перевода десятичной дроби в проценты, ее необходимо умножить на 100%.

0,27*100%=27%.

Задача 4. Вычислите: 3,8 – 2,5

Для вычитания, отнимем от дробной части дробную, а от целой целую и запишем результат (не забывайте про запятую):

• 3-2=1
• 8-5=3

Ответ: 1,3

Задача 5. Представьте в виде десятичной дроби ¼

Чтобы перевести обыкновенную дробь в десятичную, в ее знаменателе должно стоять число 10, 100, 1000 и т.д.

Поэтому необходимо преобразовать дробь ¼ в такую, в которой знаменатель будет соответствующим. Для этого умножим ее числитель и знаменатель на 25. У нас получится 25/100

25/100=0,25 (количество знаков после запятой = количеству нулей в знаменателе).

FAQ

Какая дробь называется десятичной?

Десятичная дробь – это дробь, которая записывается в строку через запятую. После запятой идет дробная часть, в знаменателе которой стоит 10, 100, 1000 и т.д., а количество цифр после пробела обозначает количество нулей знаменателя, например, 0,001 = 1/1000

Какие действия можно совершать с десятичными дробями?

С ними можно совершать все те же действия, что и с обыкновенными дробями, числами.

Для чего используются десятичные дроби?

Десятичные дроби – это более простой способ записи обыкновенных дробей, в знаменателе которых стоит 10, 100, 1000 и т.д. Ими удобнее пользоваться, например, при написании текста на компьютере.

Вывод

Десятинные дроби в ряде случаев намного более удобный инструмент, чем обыкновенные. Они используются повсеместно, поэтому владеть навыками перевода обыкновенных дробей в десятичные – просто необходимо. Примеры на десятичные дроби будут встречаться не только во всех важнейших экзаменах, с ними вы будете сталкиваться в реальной жизни.