Деление на десятичную дробь

Деление – это базовое арифметическое действие. Оно производится в отношении самых разных чисел, включая десятичные дроби. Необходимость выполнения вычислений возникает у школьников и студентов практически постоянно. Что делает актуальным вопрос о том, как правильно, быстро и точно делить десятичные дроби по правилам математики. Попробуем ответить на него максимально просто и одновременно подробно.

Основные определения

Делением называют арифметическое действие, которое обратно умножению. Оно используется в самых разных расчетах по математике, физике, химии и другим точным наукам.

Десятичная дробь представляет собой одну из самых распространенных форм записи чисел. В отличие от обычных дробей, ее знаменатель всегда выступает степенью 10. Причем число записывается без знаменателя и делится на две части - целую и дробную - которые отделяются друг от друга запятой.

Общие правила деления десятичных дробей столбиком

Стандартный способ выполнения рассматриваемой операции вручную предусматривает деление столбиком. При этом используется несколько общих и достаточно простых правил, необходимых для удобства и упрощения расчетов:

1. К десятичной дроби добавляется справа необходимое количество нулей (для получения целого числа).
2. Аналогичная операция производятся в отношении второго числа (делимого или делителя), что не приводит к изменению результата.
3. Деление столбиком выполняется по стандартной схеме.
4. После окончания деления целой части дроби, в частном ставится запятая, после чего вычисление продолжается.

Деление на целое число

Один из самых распространенных вариантов рассматриваемой задачи. Предусматривает использование указанных выше правил. Проще и нагляднее всего рассмотреть в виде примера.

Пример. Деление десятичной дроби 49,14 на 3.

Операция выполняется столбиком по описанной выше схеме и имеет следующий вид:

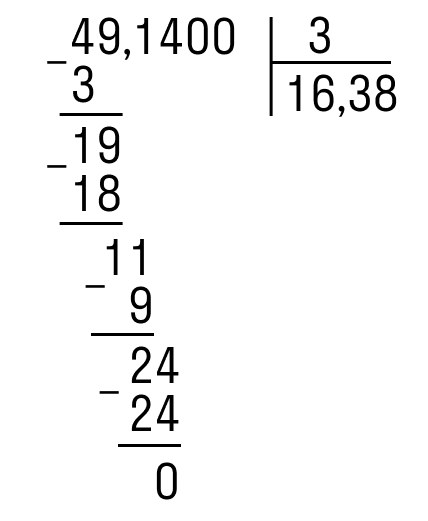
Ответ: 16,38.

Деление столбиком одной десятичной дроби на другую

Еще одна типовая задача. Ее решение предусматривает перенесение запятой в делителе для превращения его в целое число. Не стоит забывать, что аналогичным образом запятую нужно перенести и в делимом. При необходимости к нему дописываются нули. Далее производится деление на целое число, что описано в предыдущем разделе статьи.

Пример. Деление двух десятичных дробей: 6,342 на 0,21.

Решение предусматривает перенесение запятой на два знака влево (чтобы делимое стало целым числом). В результате осуществляется деление 634,2 на 21, что выглядит следующим образом:

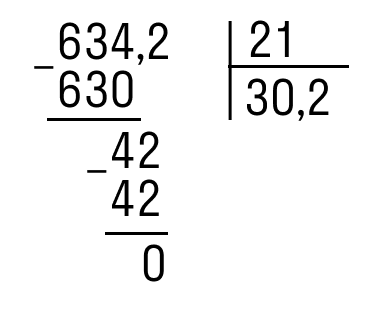
Ответ: 30,2.

Деление на 10, 100 и т.д.

Деление обратно умножению. Поэтому для того, чтобы разделить число на 10, 100 и т.д., достаточно умножить его на 1/10 (или 0,1), 1/100 (или 0,01) и т.д. Задача решается предельно просто: запятая переносится влево на количество знаков после запятой в делителе (или равное числу нулей в нем).

Примеры: 543,55 / 10 = 54,355 или 0,244 / 100 = 0,00244.

Деление на 0,1, 0,01 и т.д.

Схожая с предыдущей операция. Предусматривает замену деления на 0,1, 0,01 и т.д. на умножение на 10, 100 и т.д. Результатом становится перемещение запятой по аналогичным правилам, но не влево, а вправо. При необходимости дописывается нужное число нулей.

Примеры: 483,22 / 0,1 = 4832,2 или 0,0345 / 0,00001 = 3450.

Деление смешанного числа или обыкновенной дроби на десятичную и наоборот

Математическое действие выполняется по стандартной схеме, предусматривающей важное дополнение. Сначала все задействованный числа приводятся к единому виду – обыкновенной дроби. После чего проблем с выполнением расчетов уже не возникает.

Пример: деление смешанного числа 3 ½ на десятичную дробь 0,5.

Решение:

1. Сначала переводим все числа в обыкновенные дроби:
   • 3 ½ = 7/2;
   • 0,5 = 5/10 или 1/2;
2. Далее выполняется деление обыкновенных дробей по обычным правилам:
   • 7/2 ÷ 1/2 = 7/2 * 2/1 = 7.

Ответ: 3 ½ / 0,5 = 7.

FAQ

Как делить десятичные дроби?

Действие предусматривает использование нескольких простых правил:

1. Деление выполняется в столбик.
2. При необходимости к делителю добавляется нужное количество нулей (столько же необходимо добавить к делимому).
3. После завершения деления целой части в частном ставится запятая, а вычисления продолжаются.
4. Если в делении участвуют обыкновенные дроби или смешанные числа, для совершения операции все числа нужно сначала привести к обычным дробям.

Какие разновидности задачи встречаются на практике особенно часто?

Деление на целое число, деление десятичной дроби на другую, деление на 10, 100 и т.д., деление на 0,1, 0,01 и т.д., деление смешанного числа/обычной дроби на десятичную или наоборот.

Можно ли делить десятичные дроби на обычном калькуляторе?

Да, за исключением деления с участием смешанных числе или обыкновенных дробей. В этом случае потребуется использование специальных компьютерных программ или «продвинутых калькуляторов».

Вывод

1. Деление десятичных дробей производится столбиком (за исключением операций с участием смешанных числе и обычных дробей).
2. При необходимости к делителю и делимому добавляется нужное количество нулей.
3. После окончания деления целой части в частном ставится запятая, после чего операция продолжается.
4. Деление на 10, 100 и т.д. (как и на 0,1, 0,01 и т.д.) выполняется посредством простого переноса запятой влево (или вправо) на число, равное количеству нулей в делителе (или числу цифр после запятой).
5. Если в делении участвуют обыкновенные дроби или смешанные числа, столбик не используется. Операция выполняется по правилам для обыкновенных дробей с предварительным приведением к этому виду всех задействованных чисел.