Действительные числа

Действительные числа представляют собой широкий класс чисел, включающий как рациональные, так и иррациональные числа. Они играют важную роль в математике, физике, экономике и других науках. В этой статье мы исследуем основные свойства действительных чисел, их классификацию и практическое применение.

Основные свойства действительных чисел

Рациональные числа

Рациональные числа - это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами, а знаменатель не равен нулю. Например, 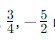 и 0.25 - рациональные числа.

Иррациональные числа

Иррациональные числа - это числа, которые не могут быть представлены в виде простой дроби и имеют бесконечное десятичное разложение без периодичности. Например, π, 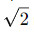 - иррациональные числа.

Бесконечность

Действительные числа могут быть как конечными, так и бесконечными. Например, конечное число 5. 5 и бесконечные числа, такие как π и .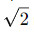

Классификация действительных чисел

• Положительные и отрицательные числа: Действительные числа могут быть положительными, отрицательными или нулевыми, в зависимости от их отношения к нулю.

Целые числа

• Целые числа включают в себя все натуральные числа, их отрицательные значения и ноль. Например,
• −3,
• −2,
• −1
• 0,
• 1,
• 2,
• 3 - целые числа.

Натуральные числа

• Натуральные числа - это положительные целые числа, начиная с единицы. Например, 1, 2, 3, 4, 5 и так далее.

Практическое применение действительных чисел

• Финансы: Действительные числа широко используются в финансовых расчетах, таких как учет доходов и расходов, инвестиции, кредиты и т. д.
• Наука: В физике и инженерии действительные числа используются для описания физических явлений, выполнения математических моделей и проведения экспериментов.
• Информатика: Действительные числа играют важную роль в информатике и программировании, используясь для хранения данных, выполнения вычислений и разработки алгоритмов.

Действительные числа образуют фундаментальную часть математического мира, являясь инструментом для описания и анализа различных явлений и процессов. Их изучение и применение позволяет нам лучше понимать мир вокруг нас и развивать новые методы и технологии в различных областях науки и промышленности.