Что такое рациональные числа
Рациональные числа — это основа арифметического мира, олицетворение упорядоченности и логики в математике. Это числа, которые выражаются в виде дробей, где числитель и знаменатель являются целыми числами, а знаменатель не равный нулю. Они расширяют понимание чисел за пределы целых чисел, включая дробные значения, которые лежат между целыми.
Мы расскажем, что такое рациональные числа, что значит иррациональное число, дадим определение, примеры задач с решениями, что такое рациональные числа в Python.
Рациональные числа – что такое, определение
Определение рациональных чисел:
Рациональные числа — это числа, которые можно представить в виде обыкновенной дроби или числа ноль. К рациональным числам относят положительные и отрицательные, целые и дробные числа, а именно: обыкновенную периодическую дробь, конечную десятичную дробь и бесконечную периодическую дробь.
Рациональные числа можно представить в виде дроби: m/n, где m является целым числом, n – натуральным числом. При этом целые числа также являются рациональными.
Например, число 0,5 можно представить как дробь 5/10 или ½, а значит, оно является рациональным. Математически это записывается как 0,5 ∈ Q.
Отрицательное число - 0,5 можно представить как отрицательную обыкновенную дробь - 5/10 или - ½, значит оно также рациональное.
Еще примеры рациональных чисел:
- десятичная дробь 2,35 = 235/100;
- отрицательная десятичная дробь – 2,35 = – 235/100
- десятичная дробь 0,25 = 25/100 = 1/4;
- целое число 8 = 8/1;
- целое отрицательное число - 8= - 8/1.
Множество рациональных чисел обозначается латинской буквой Q.
Свойство рациональных чисел
Рациональные числа обладают рядом фундаментальных свойств, которые определяют их характер и позволяют проводить разнообразные математические операции с этими числами.
Основные свойства:
- Рациональное число можно представить в виде обыкновенных дробей, где числитель и знаменатель являются целыми числами. Это позволяет компактно описывать дробные значения и проводить с ними арифметические операции.
- Плотность рациональных чисел на числовой прямой. Это означает, что между любыми двумя рациональными числами всегда можно найти еще одно рациональное число. Такая плотность обеспечивает возможность проведения интерполяции между значениями и обеспечивает удобство в решении математических задач.
- Свойства ассоциативности, коммутативности и дистрибутивности относительно основных арифметических операций: сложения, вычитания, умножения и деления. Например: переместительное свойство сложения и умножения: a+b=b+a, a*b=b*a; сочетательное свойство сложения и умножения: (a + b) +c = a + (b + c), a * b) * c = a * (b * c); распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c. Эти свойства позволяют проводить вычисления с рациональными числами, не зависящими от порядка операций, что делает их использование более удобным и эффективным.
- Рациональные числа образуют поле, что означает, что для любого рационального числа существует обратное число, которое при умножении на исходное число дает единицу. Это обеспечивает возможность проведения деления на рациональные числа и является основой для многих математических и инженерных приложений.
Иррациональные числа – определение
Определение иррациональных чисел:
Иррациональные числа – это числа, которые не могут быть выражены как отношение двух целых чисел и не могут быть представлены в виде конечной или периодической десятичной дроби. Они выражаются в виде бесконечных десятичных дробей.
Простыми словами, иррациональные числа не могут быть точно представлены в виде обыкновенной дроби и обладают бесконечной последовательностью десятичных знаков без повторяющихся цифр.
Классическим примером иррационального числа является число π = 3,1415926... которое обозначает отношение длины окружности к её диаметру. Несмотря на то, что π можно приблизить каким-либо рациональным числам, его десятичная дробь никогда не закончится и не станет периодической.
Еще примеры:
- e = 2,71828182…
- √2 = 1,41421356...
- √8 = 2.828427...
Целые vs натуральные vs рациональные
Целые, натуральные и рациональные числа – это различные классы чисел, которые используются в математике для представления и анализа количественных значений.
Чтобы не путаться, закрепим определения:
- Целые числа – это числа, включающие все натуральные числа, их отрицательные значения и ноль. Обозначаются они символом Z. Они используются для представления количественных значений, как положительных, так и отрицательных.
- Натуральные числа – это набор чисел, который начинается с единицы и продолжается до бесконечности. Обозначаются символом N. Натуральные числа используются для представления количества объектов, которые не являются дробными или отрицательными. Например, количество яблок, количество студентов в классе и т. д.
- Рациональные числа – это числа, которые можно представить в виде дроби, где числитель и знаменатель – это целые числа (за исключением знаменателя, который не должен быть равен нулю). Обозначаются они символом Q, что означает "quotient", или "частное". Рациональные числа включают в себя как целые числа, так и натуральные числа.
- Иррациональные числа – это числа, которые не могут представлены в виде дроби и имеют бесконечную и неповторяющуюся десятичную запись.
- Вещественные числа – это рациональные и иррациональные числа.
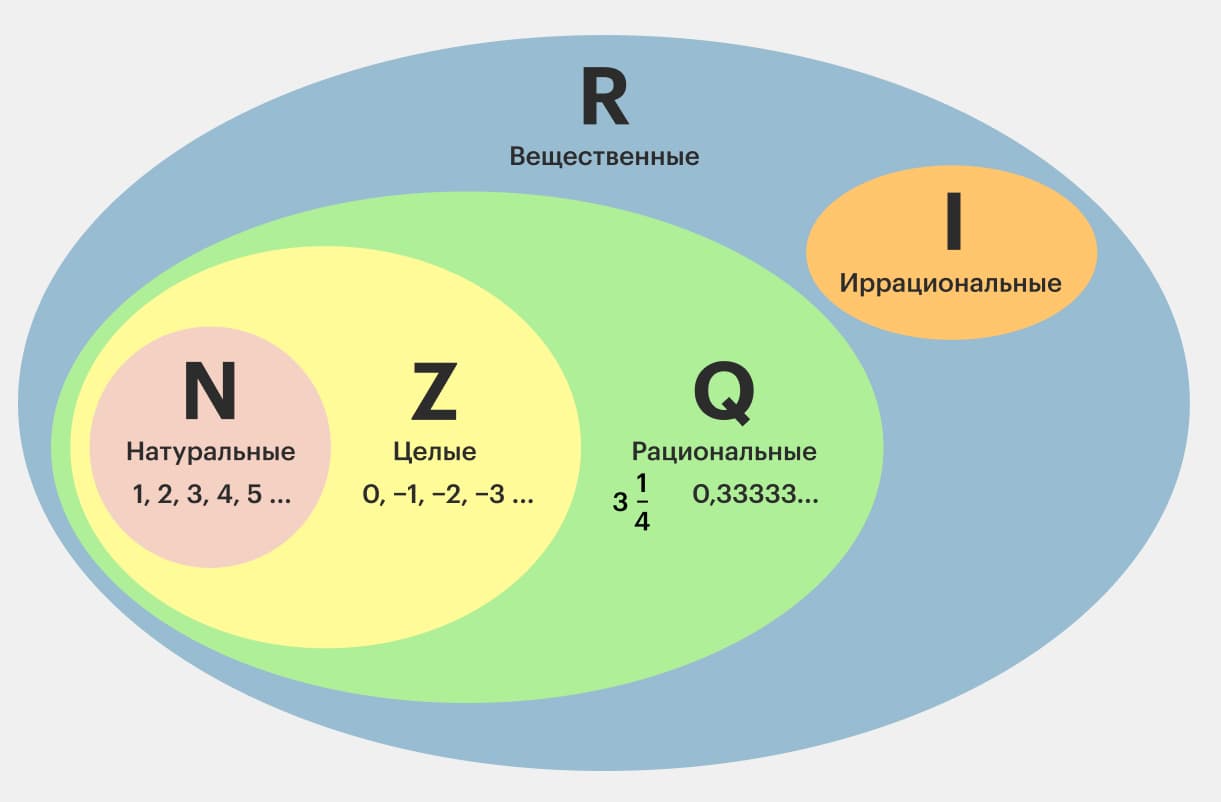
Понимать классы чисел важно для развития математического мышления, при решении различных задач.
Разберем примеры – задачи и решение
Разберем несколько задач на тему рациональные числа.
Задача №1
Даны выражения:
- √5;
- – 0,(3);
- √6.
- 23;
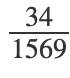
Какое их них является рациональным?
Решение:
Разберем каждое выражение:
- Корень из 5. Данное выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, значит число не рациональное.
- - 0,(3) – это бесконечная десятичная периодическая дробь, - 0,(3) =−3/10 можно представить в виде дроби, поэтому это рациональное число.
- Корень из 6 это выражение нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому это число не рациональное.
- Число 23 можно представить в виде дроби 23/1, значит оно рациональное.
- Дробь
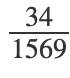 является рациональным числом.
является рациональным числом.
Ответ: рациональными являются числа под номерами 2, 3, 4.
Задача №2
Дано число √ 0,0049.
Требуется доказать, что оно рациональное.
Доказательство:
Произведем вычисления: √0,0049 = 0,07.
0,07 является рациональным числом. Что требовалось доказать.
Задача №3
Дано число в виде выражения, содержащего только рациональные числа: 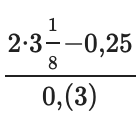
Является ли результат выражения рациональным числом.
Решение:
Нужно найти значение заданного выражения:
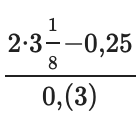 равно 18.
равно 18.
18 – рациональное число.
Ответ: значение заданного выражения является рациональным числом.
Рациональные числа в Python
На языке Python обеспечивает поддержку арифметики рациональных чисел модуль fractions.
Как создать рациональное число на Питон:
- Импортировать класс Fraction из модуля fractions.
- Указать числитель numerator и знаменатель denominator. По умолчанию numerator=0, denominator=1.

- В качестве числителя и/или знаменателя могут быть указаны другие экземпляры Fraction().

- Как из десятичного создать рациональное число.

FAQ
Будет ли рациональным числом любое простое число под корнем?
Нет. Например, любое простое число под корнем 2, 3, 5, 7, 11, 13, … не выносится из под корня и его нельзя представить в виде конечно дроби или бесконечной периодической дроби, поэтому оно не будет рациональным числом.
К какому классу чисел относится число 0?
Ноль относится к классу рациональных чисел, потому что его можно также представить в виде дроби. Так как на ноль делить невозможно, знаменатель у ноля тоже не может быть меньше единицы.
Вывод
- Рациональное число в математике — это число, которое можно представить в виде дроби, где числитель — целое число, а знаменатель — натуральное.
- К рациональным числам относятся все натуральные и целые числа, а также числа, которые можно представить в виде обыкновенных, конечных десятичных дробей и бесконечных периодических дробей.
- С рациональными числами можно проводить любые математические операции.
- Теперь вы знаете рациональные числа – это какие числа, какие они имеют свойства и чем отличаются от других классов чисел.
