Что такое квадратный корень

Алгебра – не очень сложный предмет, как скажут некоторые люди. Но когда им попадаются в задачи различные корни, они начинают искать везде помощи, ведь корни – самая сложная тема в алгебре. Сейчас мы с вами изучим всё о корнях раз и навсегда.

Квадратный корень – что это

Квадратный корень – это значение, которое даёт исходное число, умноженное на само себя. Например, 5, умноженное на само себя, даёт в итоге 25. (5 х 5 = 25). Исходя из этого, мы можем понять, что 25 – это квадратное число 5, ну а если говорить проще, то 5 – квадратный корень из 25.

Примеры квадратных чисел: 4; 9; 16; 25; 36; 49; 64; 81; 100. Большие квадратные числа и как их найти мы с вами изучим позже.

Квадратный корень vs арифметическое квадратное уравнение

Мы с вами уже узнали, что же такое квадратный корень, но ещё понятия не имеем, что же такое арифметический квадратный корень. Арифметический квадратный корень – это неотрицательное число, квадрат которого равен числу а. Число а – подкоренное число. Например, 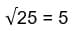. 25 – подкоренное число, иначе говоря, находится под корнем.

У арифметического квадратного корня есть всего 3 свойства.

1. Корень произведения равен произведению корней.
2. Извлечь корень из дроби – это извлечь корень из числителя и из знаменателя.
3. Чтобы возвести корень в степень, нужно возвести в степень значение под корнем.

Разница между арифметическим квадратным уравнением и квадратным корнем

Чтобы раз и навсегда понять разницу этих двух понятий, мы должны знать важное правило: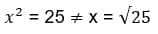 

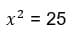 – квадратное уравнение

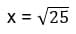 – арифметический квадратный корень

Запись рациональных чисел с помощью квадратного корня

Напомним, что рациональным числом называется число вида 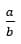, где a - целое число, а b - натуральное. Любое рациональное число можно записать как в виде обыкновенной дроби, так и в виде десятичной дроби. Иногда десятичная дробь оказывается бесконечной. Конечная десятичная дробь содержит после запятой конечное число знаков, например, число 2,03923 содержит пять знаков после запятой.

Перевод десятичной дроби в обыкновенную:

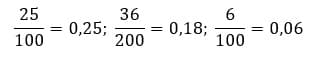
Всё, что нам нужно сделать для перевода десятичной дроби в обыкновенную дробь – поделить числитель на знаменатель дроби.

Извлечение корней

Пожалуй, самый быстрый и простой способ извлечь корень – воспользоваться таблицей квадратов. Ну разве есть способ намного проще, чтобы извлечь корень? НО! Таблицу то мы увидим, а как ею пользоваться?

Как работать с данной таблицей? Всё просто.

Например, нужно извлечь квадратный корень из .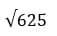

Влево – 2, вверх – 5.

Ответ: 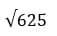 = 25.

Другие варианты:

Влево – 1, вверх – 1

Ответ: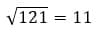 

Влево – 4, вверх – 2

Ответ: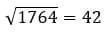 

Влево – 9, вверх – 0

Ответ: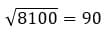 

Влево – 2, вверх – 9

Ответ: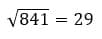 

Свойства арифметического квадратного корня

Рассмотрим свойства арифметического квадратного корня, с условием что во всех формулах и имеют положительное значение.

Основные свойства корня:

1. Корень, полученный из произведения двух и больше числе равен произведению корней таких чисел.
   
   
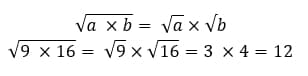
2. Корень из частного двух чисел всегда равен частому их корней. Простыми словами, корень дроби будет равен отношению корней числителя к знаменателю. При условии, что знаменатель не равен нулю.
   
   
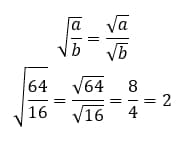
3. Корень числа в степени равен корню
   
   
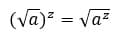
4. Корень из квадрата любого. Даже отрицательного числа, равен модулю такого числа.
   
   
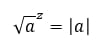
5. Возведенный в квадрат корень всегда равен возводимому числу или выражению
   
   

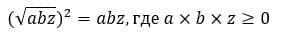
Умножение арифметических корней

Не зря же мы с вами научились пользоваться таблицей квадратов, да? Для изучения этой темы, таблица квадратов нам будет служить как правая рука. Так что, пожалуйста, не забывайте использовать ее в своих работах.

Для умножения арифметических корней нам нужно знать только одну формулу:

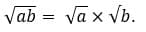
Например,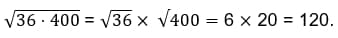 

Ответ: 120.

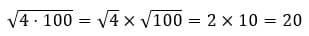
Ответ: 20.

Рассмотрим уравнение, в котором нет возможности извлечь корни из чисел:

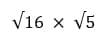
Не нужно нервничать, увидев это уравнение. Сначала решаем как научились ранее: 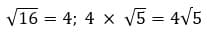. Если нет возможности извлечь корень из числа, то записываем без изменений.

Ответ: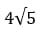 

Примеры: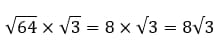 

Ответ: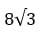 

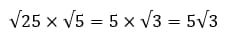
Ответ: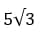 

А что, если множителей больше, чем двух? Нервничать тоже не стоит! Поступаем так же, как и с двумя множителями.

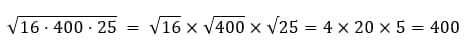
Ответ: 400.

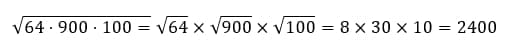
Ответ: 2400

Деление арифметических корней

Деление и умножение арифметических корней сами по себе похожи. Давайте попробуем убедить вас в этом. Для деления арифметических корней, нам нужно знать лишь одну формулу:

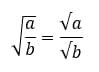
Например,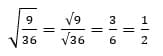 

Ответ: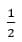 

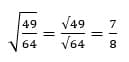
Ответ: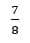 

В делении так же могут попасться смешанные дроби:

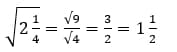
Ответ: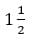 

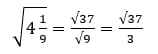
Ответ: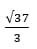 

Выполняя действие деления, не стоит забывать сокращать множители.

Возведение арифметических корней в степень

Переходим с вами на более сложный этап изучения тем. Возведение арифметических корней в степень совсем не сложное. Давайте пытаться разобраться. Для возведения арифметического корня в степень, нам опять нужно запомнить раз и навсегда одну формулу: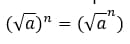 

Например,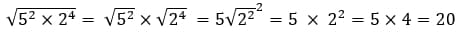 

Для следующего примера пригодится формула: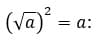 

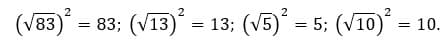
Так же нужно запомнить формулу: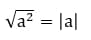 

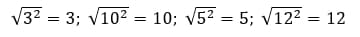
Чтобы решать такие примеры без какой-либо паники, нужно лишь повторить свойства степеней.

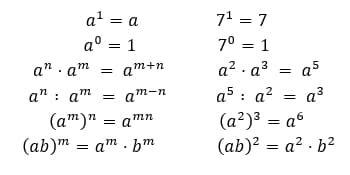
Внесение множителя под знак корня

Итак, мы с вами уже знаем как умножать, делить и возводить в степень квадратные корни. Но теперь у нас на пути встала одна из сложных задач – внесение множителя под знак корня. Звучит страшно, не так ли? Но если мы сейчас с вами наберёмся терпения и заучим нужные формулы, то для нас эта тема не будет помехой.

Как же вносить множитель под знак корня? Для этого нам нужно запомнить ещё одну формулу: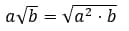 

Кажется, что эта формула самая лёгкая.

Для изучения этой темы нам так же пригодится ранее изученная формула: 

Возьмём выражение: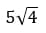 

1. Извлечём квадратный корень и умножим его на 5.

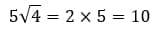
В данном выражении число 5 – множитель.

Запомните, что вносить множитель под знак корня нужно обязательно так, чтобы значение исходного выражения осталось неизменным. Нельзя вносить отрицательные числа под знак корня.

Вспоминая формулу , мы можем понять, что число 5 должно быть возведено во вторую степень.

2. 

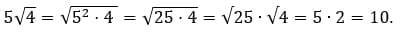
Вынесения множителя из под знака корня

Итак, как вносить множитель под знак корня мы с вами научились. Переходим к другому, более, так скажем, сложному этапу. Не волнуйтесь, совсем скоро мы уже изучим все самые сложные темы и сможем расслабиться.

Быстренько потренируемся извлечь корень из имеющихся множителей, чтобы дальше работать было легче.

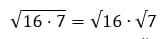
В данном выражении мы можем извлечь квадратный корень только из 16, поэтому:

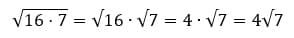
Вот мы с вами и научились выносить множитель из-под корня. Легко, правда?

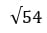 – Раскладываем подкоренное выражение на множители:

54 = 9 × 6 – Извлекаем корень из 9. Множитель 6 оставляем под знаком корня.

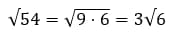
Ответ: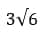 

Примеры выражений:

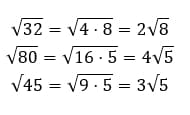
Извлечение квадратного корня из большого числа

Ранее мы с вами изучали квадратные корни и учились пользоваться таблицей квадратов. Сейчас нужно вспомнить всё изученное, ведь таблица квадратов – наша правая рука. Но есть одна проблема. Таблица квадратов заканчивается на “9801”, а что, если нам попадётся число намного больше? Сейчас будем разбирать эту проблему, чтобы она не преграждала наш путь знаний.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

1. Определить сотни, между которыми оно стоит.
2. Определить десятки, между которыми оно стоит.
3. Определить последнюю цифру в этом числе

Извлечём корень из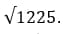 

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

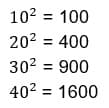
Мы видим, что 1225 больше 900, но меньше 1600.

Это значит, что число 1225 находится между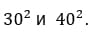 

Применим в работе ещё одну таблицу.

Как же пользоваться этой сложной таблицей?

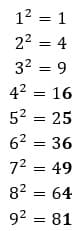
Теперь вернёмся к нашему выражению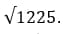 

31, 32, 33, 34, 35, 36, 37, 38, 39, 40

Работаем по таблице. В нашем выражении последним идёт цифра 5, значит 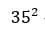 – это то, что нам нужно.  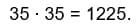Всё сходится.

Если для вас данный способ показался совсем не понятным – не отчаивайтесь. Есть еще один способ, более понятный – разложить число на множители. Для этого способа, конечно, пригодится намного больше времени, но что поделать?

Возьмём выражение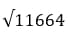 

Разложим на множители:

11664:4 = 2916

2916:4 = 729

729:3 = 243

243:3 = 81

1

Запишем выражение в следующем виде:

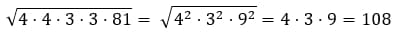
Ответ: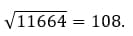 

Конечно, решать такие выражения лучше всего при помощи онлайн-калькулятора или же обычного. На эту тему мы с вами и поговорим.

Задачи и примеры

1. Вычислите значения квадратных корней: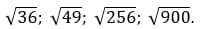 

Как решаем: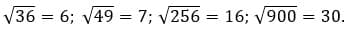 

Ответ: 6; 7; 16; 30.

2. Вычислите значения квадратных корней: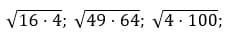 

Как решаем: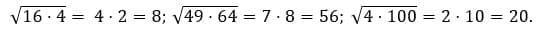 

Ответ: 8; 56; 20.

3. Вычислите значение выражения: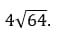 

Как решаем: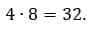 

Ответ: 32.

4. Вычислите значение выражения: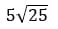 

Как решаем: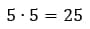 

Ответ: 25.

5. Вычислите значение квадратного корня: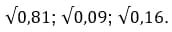 

Как решаем: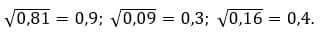 

Ответ: 0,9; 0,3; 0,4.

6. Вычислите значение выражения: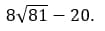 

Как решаем: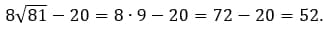 

Ответ: 52.

7. Вычислите значение выражения: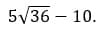 

Как решаем: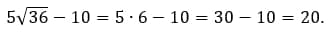 

Ответ: 20.

8. Внесите множитель под знак корня: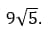 

Как решать: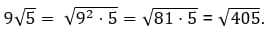 

Ответ: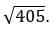 

9. Вынесите множитель из-под знака: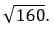 

Как решаем: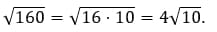 

Ответ: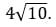 

10. Найдите значение выражения: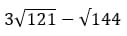 

Как решаем: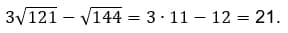 

Ответ: 21.

Онлайн-калькуляторы – обзор

Так как калькуляторы важны всем, даже самым лучшим и умным математикам – люди придумали онлайн-калькуляторы. Но что, если вникнуть в историю калькуляторов? С древнейших времён человечество освоило счет и для его упрощения использовало все, что только могло. Вначале в ход шли пальцы на руках и ногах. Когда пальцев стало не хватать, люди начали искать различный вспомогательный счетный материал: палочки, камушки, ракушки, – кто, что находил. Но, со временем понадобилось устройство, которое можно было бы носить с собой и использовать, как говориться, в походных условиях. Тогда и придумали калькулятор, но конечно же не сразу. Долгие годы эволюции, и человечество уже придумывает сложные, загадочные технологии. Что же нас ждёт в будущем? Покажет только время.

Итак, пришло время обзора онлайн-калькуляторов.

• https://calc.loviotvet.ru/

Чем же этот онлайн-калькулятор хорош? Основное отличие от других калькуляторов – это наличие продвинутых возможностей, типа вычислений, работы со сложными тригонометрическими функциями и так далее. Для начала нам нужно ввести точный и верный пример или задание, которое мы хотим решить, после чего нажимаем на кнопку “Ответ” и расписанное решение появится сбоку. Есть как и ПК версия, так и мобильная.

• https://ru.symbolab.com

Пожалуй, этот калькулятор – самый лучший, который я когда-либо видела. Почему? Убедитесь сами. Когда вы переходите на сайт этого калькулятора, сверху есть множество кнопочек. “Калькулятор”, “Решения”, “Графика”, “Геометрия”, “Шпаргалки” и так далее. Даже есть обычная алгебра, линейная, Пре алгебра. Имеется химия, экономика и прочее. Матрицы, тригонометрия, статистика, исчисление тоже в счету. Мечта, а не сайт. Конечно, есть платные функции, но в бесплатных тоже можно понять многое и без подробного решения и вычисления.

• https://calc.by/

Последний калькулятор, который входит в топ 3 лучших. На этом сайте вы можете найти не только обычный математический калькулятор, а ещё калькуляторы веса и калорий, калькуляторы для беременных, калькулятор дней, расстояний и топлива, таможенный калькулятор и многие другие. Содержит ОЧЕНЬ хороший набор научных калькуляторов.

FAQ

Как подготовиться к контрольной работе по теме?

Главное разобраться с определением. Если нет понимания что √3 = 9 — это неверно, да должно быть наоборот, тогда лучше позаниматься с репетитором.

Почему корни изучают в 8 классе, а не в 10 ведь тема сложная?

Согласно школьной программе, предполагается, что учащиеся уже изучили натуральные, рациональные и целые числа. Решили много примером и успели приобрести навыки использовании формул сокращенного умножения и алгебраических дробей. Именно в этот момент предполагается переход от множества рациональных чисел к иррациональным, какими являются числа под знаком корень.

В заданиях ОГЭ и ЕГЭ встречаются задачи с вычислением корней?

Каждый год в заданиях ОГЭ не менее 6 задач на тему «Арифметический квадратный корень». Задания просты и достаточно понимания определения. В ЕГЭ таких заданий 7. Профильную математику без знания корней сдать нельзя, ведь из 19 заданий 17 содержит примеры на вычисление корня.

Мы изучили все темы из разряда квадратные корни и хочется сказать то, что квадратные корни и арифметические квадратные корни – это очень сложная тема. Это не примеры типа 5+5=10, а уже более серьёзные и умные темы, которые затрагивают в старших классах. Главное не забывать то, что главная таблица в алгебре, которая поможет везде – это таблица квадратов, палочка-выручалочка.