Что такое гипербола
Гипербола - это геометрическая фигура, которая представляет собой множество точек на плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек, называемых фокусами, постоянна.
Гипербола имеет две ветви, которые расходятся от центра, который является точкой пересечения осей симметрии. Оси симметрии гиперболы называются главными осями, и они пересекаются в центре гиперболы. Фокусы находятся на главной оси, и расстояние между фокусами называется фокусным расстоянием.
Уравнение гиперболы
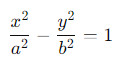
где a и b - полуоси гиперболы.
Пример решения
Построить гиперболу, заданную уравнением 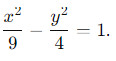
Шаг 1: Определим оси симметрии гиперболы. В данном уравнении 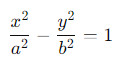 , поэтому ось x - главная ось, а ось y - второстепенная.
, поэтому ось x - главная ось, а ось y - второстепенная.
Шаг 2: Найдем фокусы. Используем формулу для фокусного расстояния: 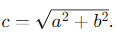 В нашем случае
В нашем случае 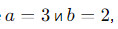 поэтому
поэтому 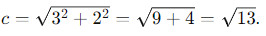
Шаг 3: Построим гиперболу на координатной плоскости, используя фокусы и размеры осей. Для этого начнем с рисования прямоугольника с центром в начале координат, ось x будет проходить через его длинные стороны, а ось y - через короткие стороны. Затем проведем асимптоты гиперболы (линии, к которым гипербола стремится на бесконечности), которые проходят через центр гиперболы и фокусы.
Шаг 4: Найдем точки пересечения гиперболы с осями координат. В нашем случае гипербола пересекает ось x в точках (±3,0) и ось y в точках (0,±2).
На графике будет видно, что гипербола имеет две ветви, которые расходятся от центра. Ось x является главной осью, а ось y - второстепенной. Гипербола пересекает оси координат в четырех точках, которые были вычислены ранее.
