Четные и нечетные числа
Четные и нечетные числа - это категории натуральных чисел, которые можно определить следующим образом:
Четные числа
- Число называется четным, если оно делится на 2 без остатка, то есть если остаток от деления на 2 равен нулю. Формально, число n является четным, если существует целое число k, такое что n=2⋅k.
Примеры четных чисел: 2, 4, 6, 8, 10, …
Нечетные числа
- Наоборот, число называется нечетным, если оно не делится на 2 без остатка, то есть если остаток от деления на 2 не равен нулю. Формально, число n является нечетным, если существует целое число k, такое что n=2⋅k+1.
Примеры нечетных чисел: 1, 3, 5, 7, 9, …
Свойства четных и нечетных чисел
- Сложение четных чисел:
- Сумма двух четных чисел всегда четна. Например, 2+2=4.
- Сложение нечетных чисел:
- Сумма двух нечетных чисел всегда четна. Например, 3+5=8.
- Сложение четного и нечетного чисел:
- Сумма четного и нечетного числа всегда нечетна. Например, 2+3=5.
- Умножение четных чисел:
- Произведение двух четных чисел всегда четно. Например, 2×4=8.
- Умножение нечетных чисел:
- Произведение двух нечетных чисел всегда четно. Например, 3×5=15.
- Умножение четного и нечетного чисел:
- Произведение четного и нечетного числа всегда четно. Например, 2×3=6.
- Деление на 2:
- Если число делится на 2 без остатка, оно является четным. Например, 4 и−10.
- Если число не делится на 2 без остатка, оно является нечетным. Например, 5 и −7.
- Возведение в степень:
- Четное число возведенное в любую степень всегда четно. Например,
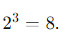
- Нечетное число возведенное в нечетную степень всегда нечетно. Например,
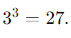
- Нечетное число возведенное в четную степень всегда четно. Например,
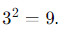
- Четное число возведенное в любую степень всегда четно. Например,
Эти свойства часто используются при арифметических операциях и в различных математических доказательствах.

