Центральные и вписанные углы

Угол – одна из самых известных геометрических фигур. Он образован выходящими из одной точки двумя лучами. Угол часто используется вместе с другими фигурами, включая окружность. Что позволяет получить на выходе центральный и вписанный углы. Рассмотрим определение каждого, их основные свойства и примеры задач из школьного курса геометрии вместе с решением.

Центральный угол и вписанный угол

Определение угла дано выше – во вступлении к статье. Здесь же имеет смысл привести значение трех других терминов, ключевых для рассматриваемой темы.

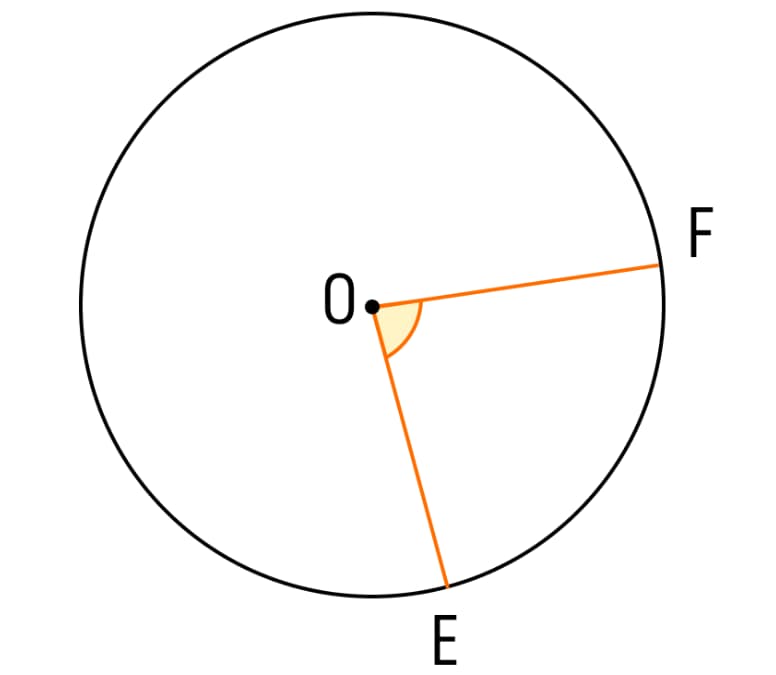
Окружностью называют замкнутую линию, любая из точек которой одинаково удалена от центра. Именно в центре располагается вершина центрального угла. Причем его значение равняется дуге (это часть окружности между лучами угла), на которую угол опирается. На приведенном ниже рисунке центральный угол обозначается как EOF, а опорная дуга – EF.

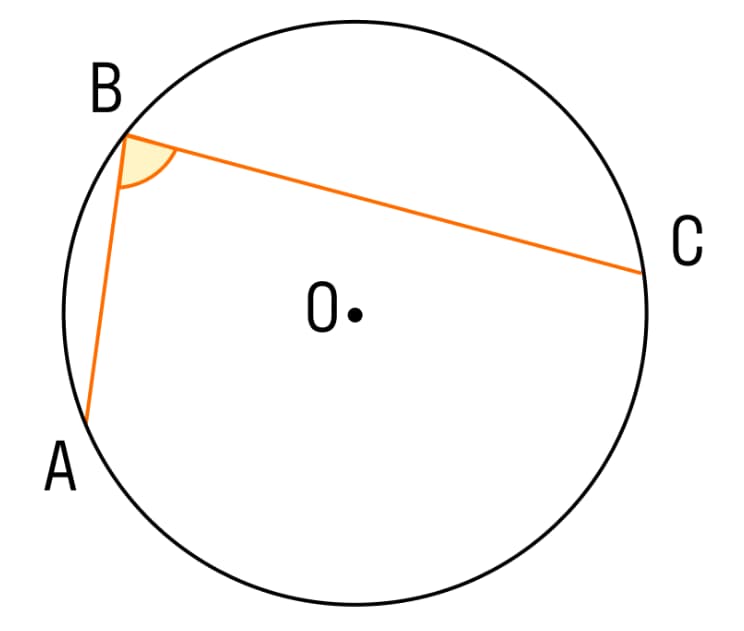
Вписанный называют угол с вершиной, расположенной непосредственно на окружности. В этом случае его величина равняется половине опорной дуги. На рисунке угол вписанный угол обозначен как ABC, а дуга – как АС. Центра окружности на обоих рисунках отмечен О.

Основные свойства центрального и вписанного угла

Несмотря на визуальную простоту определения и изображения каждого из рассматриваемых углов, их свойства активно используются в геометрии для решения разнообразных задач. Наиболее значимыми из них выступают такие:

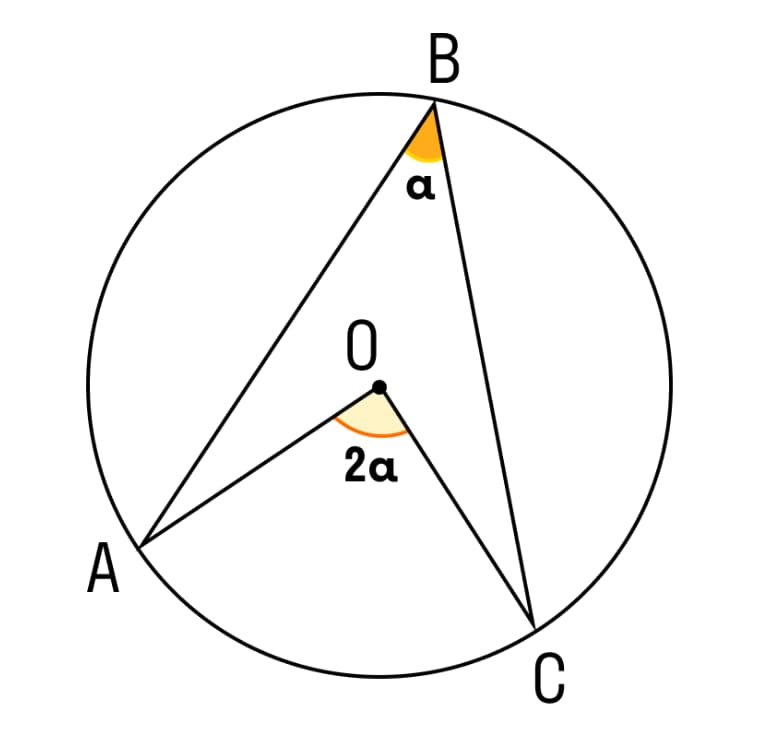
1. При опоре на одинаковую дугу центральный угол в два раза больше, чем вписанный.
   
   
2. Базовая теорема центрального угла. Его значение равняется градусной мере опорной дуги.
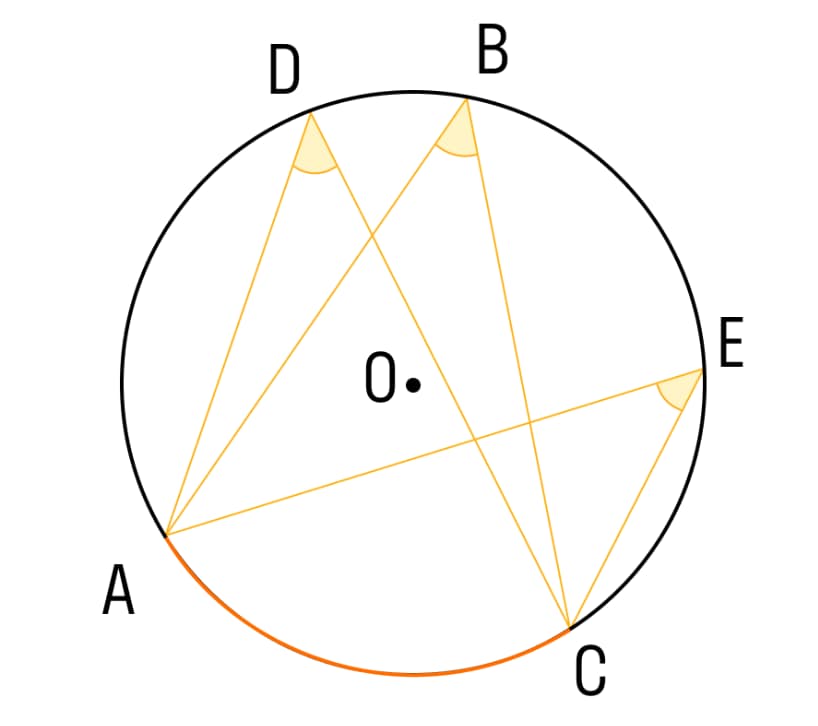
3. Все вписанный углы, которые опираются на одинаковую дугу, равняются друг другу (на рисунке ниже – углы с вершинами в точках D, B и Е).
   
   
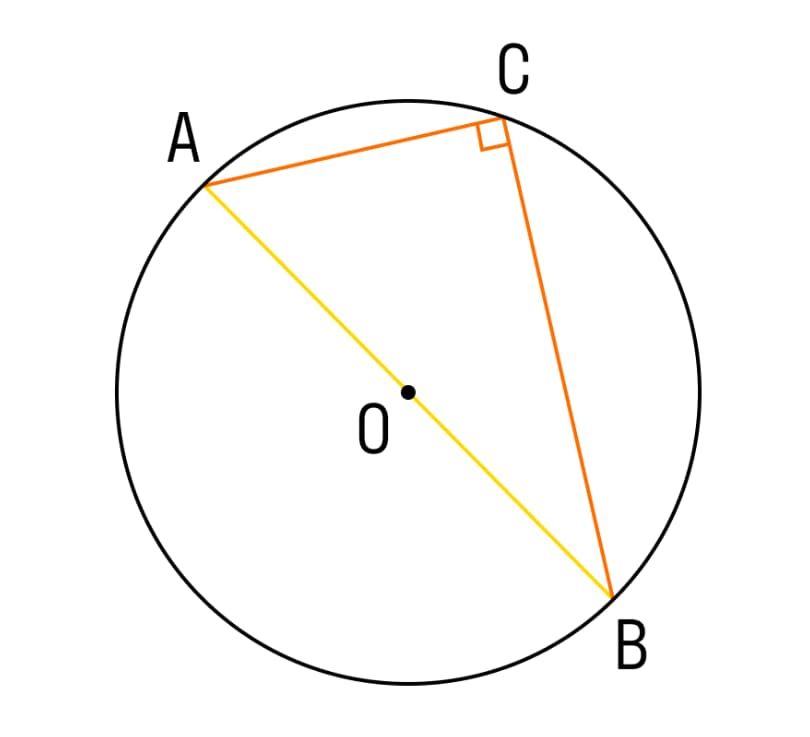
4. Если вписанный угол опирается на диаметр, он равняется 90 градусам, то есть является прямым.
   
   

Наличие вписанного угла означает возможность построения описанного. Если первый находится внутри окружности, то второй – за ее пределами. Общей для обоих видов угла характеристикой выступает соприкосновение лучей с окружностью. На рисунке ниже описанный угол имеет вершину в точке А и соприкасается с окружностью в точках В₁ и С₁.

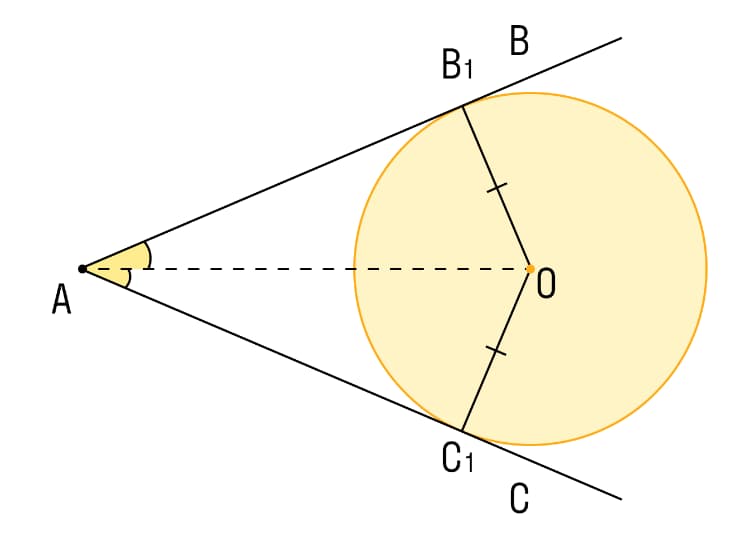
Важно отметить, что биссектриса описанного угла проходит через центр окружности. То есть делит его на две равные части.

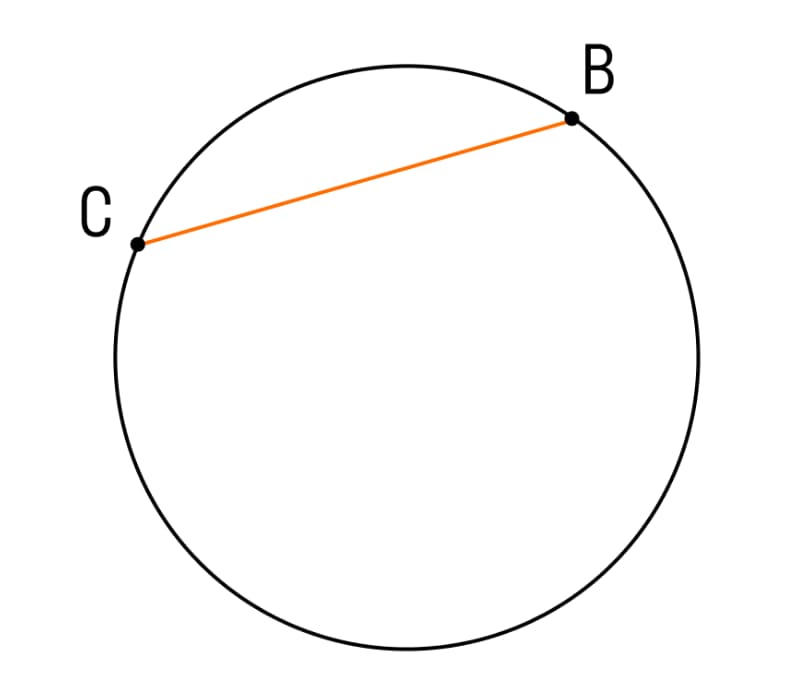
В качестве дополнительного термина, который также очень пригодится для решения задач, необходимо привести еще один. Речь идет о хорде, представляющей собой отрезок, который соединяет две точки, расположенные на окружности. Пример хорды представлен ниже и обозначается как BC.

Используя приведенное выше определение, можно сформулировать несколько важных характеристик хорды:

1. При пересечении двух хорд внутри окружности, произведения отрезков для каждой из них равны (АВ*АС = AD*AE).
   
   
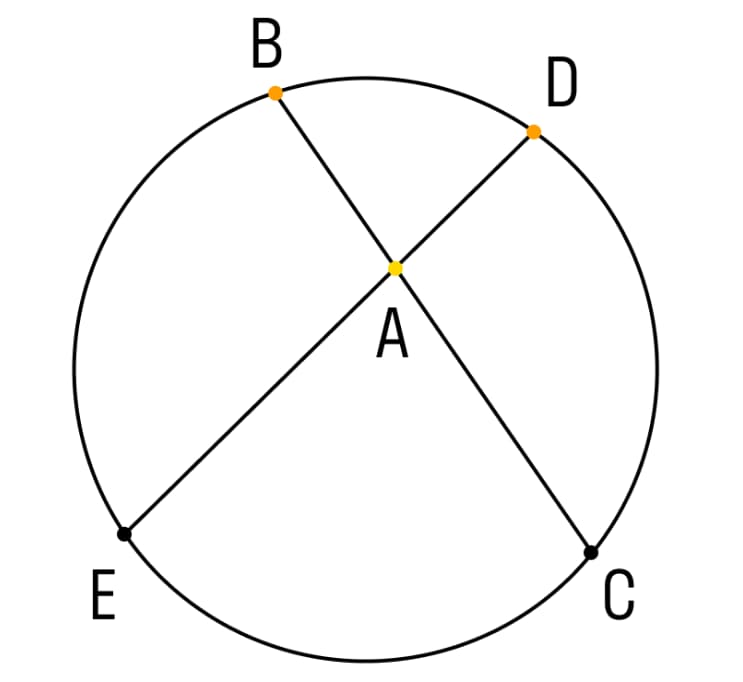
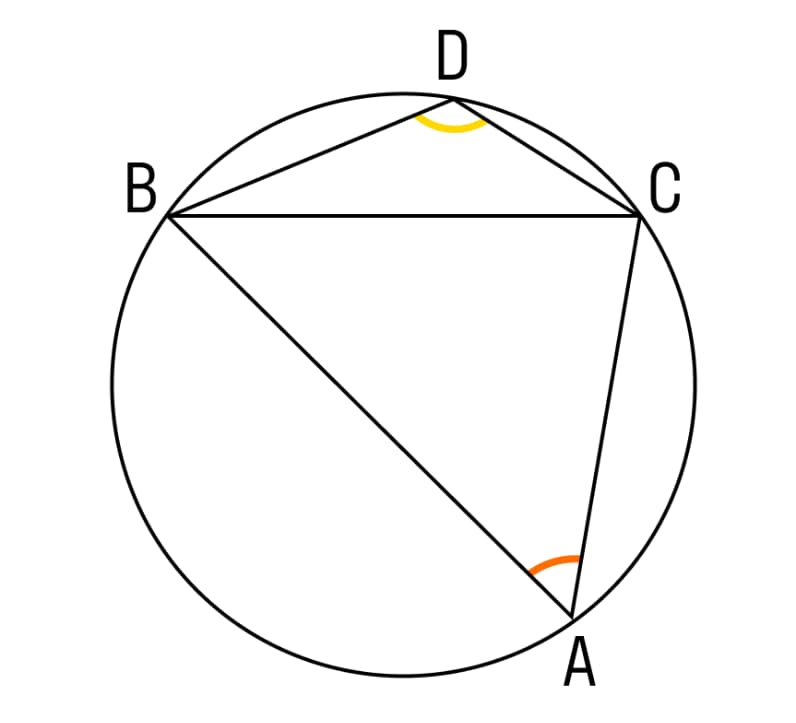
2. Вписанные углы, опирающиеся на одну хорду и имеющие вершины, расположенные с одной стороны хорды, равны друг другу.
   
   
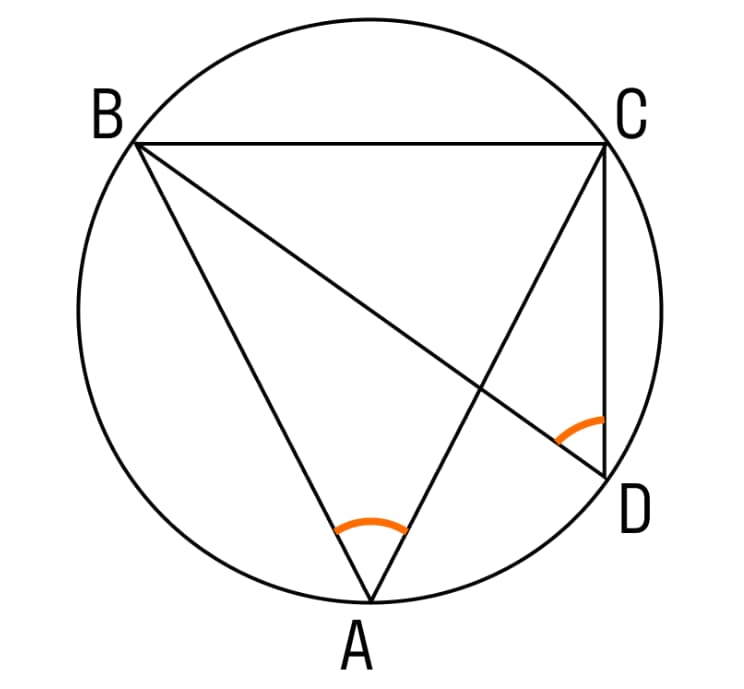
3. Сумма двух вписанных углов, опирающихся на одну хорду и имеющих вершины, расположенные с разных сторон хорды, равняется 180 градусам.
   
   

Задачи и их решение – примеры

Изложенный выше теоретический материал активно используется для решения различных задач. Приведем несколько примеров.

Задача №1. Имеется окружность. Внутри расположен вписанный угол АВС. Дуга АС равняется 180 градусам. Дуга ВС равняется 90 градусам. Найти значение вписанного угла.

Решение задачи предусматривает использование теоремы вписанного угла. Сначала определяется значение опорной дуги, которое равняется 360 – 180 – 90 = 90 градусов. В соответствии с теоремой, величина вписанного угла равняется половине опорной дуги, то есть 45 градусам.

Ответ: 45 градусов.

Задача №2. В окружность расположены два угла: центральный и вписанный. Оба опираются на одну дугу. Первый равняется 150 градусам. Каково значение второго?

Решение основано на свойстве центрального угла и теореме о вписанном. Исходя из первого, градусная мера опорной дуги равняется центральному углу, то есть составляет 150 градусов. Теорема гласит, что вписанный угол составляет половину опорной дуги. То есть равняется 75 градусам.

Ответ: 75 градусов.

FAQ

Чем отличаются и чем похожи центральный и вписанный углы?

Оба угла связаны с окружностью. Вершина первого располагается в ее центре. Второго – непосредственно на окружности. Оба угла опираются на часть окружности, которая называется дугой.

Для чего они используются?

Оба типа углов активно применяются для решения разнообразных теоретических и практических задач. Как в процессе обучения, так и в различных сферах профессиональной деятельности.

Можно ли для решения задач с использованием центральных и вписанных углов использовать онлайн-калькуляторы?

Онлайн-сервисы с подобным функционалом можно найти в интернете. Но их использование несколько затруднено разнообразием задач, исходные условия которых предусматривают присутствие центральных и вписанных углов. Пример такого калькулятора - https://allcalc.ru/node/594.

Вывод

1. Центральным называют угол, вершина которого расположена в центре окружности.
2. Вписанным называют угол, вершина которого расположена непосредственно на окружности.
3. Оба типа углов часто используются для формулирования и решения разнообразных геометрических, инженерных и технических задач.