Больше, меньше, равно

Сравнение величин – важнейшая составляющая курса математики начальной. Чтобы школьникам правильно сопоставлять числа, им следует научиться оперировать знаками «больше», «меньше», «равно».

Сравнение величин в математике

Сравнение величин в математике – это тема, которая изучается с 1 класса общеобразовательной школы. Обучаясь сравнивать, школьники развивают чувство чисел – способность распознавать и находить взаимозависимости между ними. Так формируются первичные навыки анализа и упорядочивания сведений.

Чтобы сравнивать величины, в математике используются 3 базовые символа:

Знаки «больше» и «меньше»

Знаки «больше» и «меньше» используются для сравнения двух чисел (или математических выражений) и показывают, какое из них имеет большее и меньшее значение.

Символы используются в неравенствах и указывают одновременно на большие и меньшие величины.

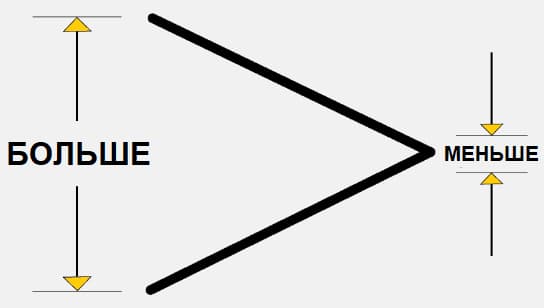
Иными словами, Широкий конец символа всегда обращён к большему числу (математическому выражению). Соответственно, стрелка указывает на меньше число.

Как запомнить знаки

Школьникам сложно сразу запомнить, в какую сторону развёрнут широкий и узкий конец у символов «больше» и меньше». И если этот навык не закрепляется, то он сохраняется в средней и старшей школе.

Чтобы запомнить знаки, есть разные способы:

1. Метод точек. Числа, подлежащие сравнению, записывают в одной строке, оставляя между ними свободную ячейку. Затем возле большей величины ставят двоеточие, возле меньшей – точку (поскольку 2 точки больше 1). Соединяют их так, чтобы получился символ «<» или «>».
   
   
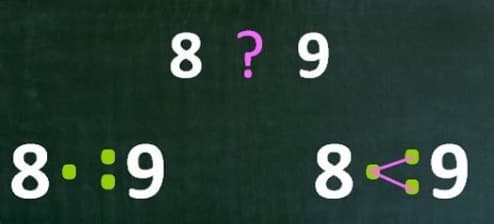
2. Метод «Аллигатора». Ребёнку легче понять и усвоить информацию с помощью образов, что и предлагает этот способ. Знаки «больше» и «меньше» следует представить в виде пасти аллигатора, а цифры слева и справа – в виде маленьких рыбок. Аллигатор всегда желает съесть большее количество пищи, поэтому его пасть раскрыта в сторону большего числа.
   
   
3. Метод записи чисел. Это мало употребляемый, но эффективный способ запоминания математических символов сравнения. Его принцип прост: при перечеркивании нижнего элемента знак «больше» становится похож на цифру 7, знак «меньше» – на 4. Это логично, т.к. 7 больше 4.
   
   

Примеры использования символов «больше» и «меньше»

Сравнение натуральных чисел

При сравнении натуральных чисел важно понимать, что такое разрядность в математике. поэтому перед освоением неравенств изучите, как оперировать ей.

Алгоритм сравнения:

1. Разложите натуральное число по разрядам, представьте данные в табличной форме.
   
   
2. Последовательно сравнивайте разрядные слагаемые (продвигаясь от наибольшего к наименьшему), пока не найдёте различающиеся числа.
   
   
3. Правильно запишите неравенство.
   
   

Сравнение десятичных дробей

При сопоставлении десятичных дробей также необходимы навыки их разложения на разряды. Но в целом процедура не отличается от сравнения натуральных чисел.

Алгоритм сравнения:

1. Разложите десятичную дробь по разрядам, представьте данные в табличной форме.
   
   
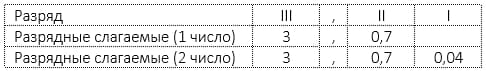
2. Последовательно сравнивайте разрядные слагаемые (продвигаясь от наибольшего к наименьшему), пока не найдёте различающиеся числа.
   
   
3. Правильно запишите неравенство.
   
   

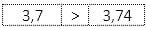
Сравнение простых дробей

Простые дроби сравнивать немного сложнее. Здесь важно сопоставить знаменатели и числители, и в зависимости от полученных результатов выбрать алгоритм.

Следуйте инструкции:

1. Сравните числители и знаменатели простых дробей: равны ли они?
   Представленные дроби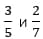  не имеют одинаковых числителей или знаменателей.
2. Используйте эквивалентные дроби, найдя общий знаменатель (для этого умножьте каждую дробь на противоположный знаменатель).
   
   
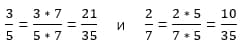
3. Сравните эквивалентные дроби, чтобы определить, какая из них больше. Запишите ответ, используя исходные числа.
   Чтобы наглядно представить дроби, изобразите 2 одинаковые фигуры (прямоугольники) и разделите их на 35 равных частей; в каждой заштрихуйте столько ячеек, сколько указано в соответствующем знаменателе: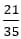  занимает 21 часть, а  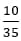– 10 частей; значит,  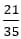больше .
   
   
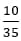   Ответ: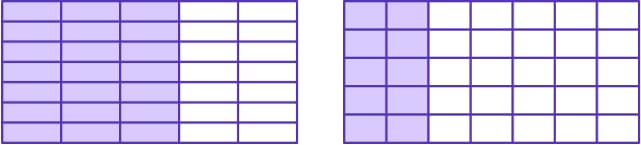 

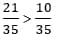
Если дроби имеют одинаковые числители, то процедура сравнения упрощается. В таком случае применяется правило: чем меньше знаменатель, тем больше каждая часть целого и наоборот.

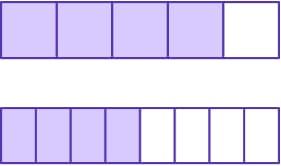
Например, 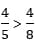, поскольку они имеют идентичные числители, а знаменатель первой дроби меньше. Это можно ясно увидеть, ели представить числа графически:

Знак равенства

Если величины совпадают, то при их сравнении применяется знак равенства. Он указывает на то, что 2 числа (или математические выражения) в левой части полностью идентичны.

Знак равенства изображается в виде 2 параллельных чёрточек, например, как в этом выражении:

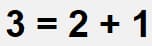
FAQ

Как быстро запомнить знаки «больше» и «меньше»?

Чтобы запомнить символы «больше» и «меньше» быстро и эффективно, нужно сначала понять, что широкий конец всегда указывает на большую величину. И в силу того, что в неравенствах первое число (математическое выражение) сравнивается со вторым, символ > означает «больше», а символ < – меньше.

Какие варианты символов «больше» и «меньше» существуют?

В уравнения с неизвестными встречаются знаки «больше или равно» и «меньше или равно», которые обозначаются символами ≥ и ≤ соответственно. Они указывают на неопределённость результата: величины или отличаются или идентичны. Чтобы это узнать, нужно решить неравенство.

Вывод

Сравнение – это процесс сопоставления свойств различных объектов. Оно является важным компонентом нашей жизни, т.к. позволяет познавать и совершенствовать себя и окружающий мир. Поэтому сравнение величин в математике – одна из базовых тем, которые осваиваются в начальной школе.

Школьникам необходимо осознать смысл знаков «меньше» и «больше», научиться правильно оперировать ими. Это простая тема, но она требует тщательной отработки навыка сравнения. Это позволит ученику быстро и эффективно ориентироваться в мире чисел.