Арифметическая прогрессия

Арифметическая прогрессия – это одна из основных числовых последовательностей, которая чаще остальных используется в математике. Она выражается простой и понятной формулой.

Определение числовой последовательности

В математике числовая последовательность – это некоторое множество чисел, упорядоченное согласно постоянным закономерностям и правилам.

Если согласно некоторой закономерностью каждому натуральному числу n соответствует строго определённое число x_n, то говорят, что задана числовая последовательность {x_n}: x₁, x₂, x₃, …, x_n. Иначе говоря, числовая последовательность является функцией натурального аргумента: x_n = f(n).

На практике задать последовательность можно несколькими способами:

1. Словесно. Закономерность, определяющая порядок членов последовательности, озвучивается устно. Например, можно сказать так: «Задана последовательность простых чисел: 3, 6, 9, 12, 15...».
2. Аналитически. Указывается формула общего члена последовательности по образцу: x_n = f(n).
3. Рекуррентно (посредством рекурсии). Здесь указывается первый элемент и общий алгоритмы вычисления остальных членов последовательности. Например, при x₁ = 10 и x_n+1 = a_n + 10 говорят, что задана последовательность с первым членом 10 и разностью 10.
4. Графически. Последовательность значений отображают в виде точек на координатной плоскости, соответствующих значения на оси 0x (абсцисс).

Определение арифметической прогрессии

Арифметическая прогрессия – это последовательность чисел, в которой разница между соседними членами является константной (постоянной величиной).

Представим любую арифметическую последовательность наглядно:

Здесь представлен ряд последовательных натуральных чисел, разность (d) между которыми равна 5. В этом легко убедиться, вычитая из каждого члена предыдущее значение: d = 10 – 5 = 5, d = 15 – 10 = 5 и т.д.

Последовательность принято обозначать буквами латинского алфавита. Каждый её член также записывается буквой, но с индексом, соответствующим его порядковому номеру в ряду.

При формулировании условий задач часто говорят об N-ном члене арифметической последовательности, который выражается числом с порядковым номером n: a_n.

Также арифметическую прогрессию можно определить, как последовательность чисел, в которой для каждой пары последовательных членов второе число получают путём прибавления фиксированного числа к первому. Так, в описанной выше арифметической последовательности (1, 2, 3, 4, 5, 6,…, n) каждое число получают путём прибавления 1 к предыдущему, например, 1 + 1 = 2, 2 + 1 = 3, 3 + 1 = 4 и т.д.

Если обобщить приведённую информацию, то можно сказать, что арифметическая прогрессия представляет собой последовательность типа a₁, a₂,..., a_n, в которой для каждого натурального n соблюдается равенство:

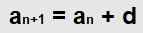
Свойство арифметической прогрессии

Арифметическая прогрессия обладает множеством свойств. Среди их многообразия можно выделить те, которые на практике используются чаще всего:

1. Каждый член (x_n) последовательности равен предыдущему, увеличенному на общую разность (a). Это выражается унифицированной формулой x_n+1 = x_n + a.
2. Элемент x_n представляет собой среднее арифметическое значение 2 соседних членов последовательности, что можно выразить как x_n = (x_n-1 + x_n+1) / 2.
3. Три числа x, y, z принадлежат последовательности, если выполняется равенство 2y = x + z.

Формула n-го члена арифметической прогрессии

Основываясь на базовом определении арифметической прогрессии, можно сделать закономерный вывод, что для неё выполняется следующее правило:

a₂ – a₁ = a₃ – a₂ = a₄ – a₃ = … = a_n – a_n-1 = d

Отсюда выведем формулы каждого (кроме первого) члена последовательности:

a₂ = a₁ + d

a₃ = a₂ + d = (a₁ + d) + d

a₄ = a₃ + d = (a₂ + d) + d = ((a₁ + d) + d) + d = a₁ + 3d и т.д.

Мы можем унифицировать эту запись и получить формулу n-ого члена арифметической прогрессии:

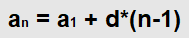
FAQ

Как понять, что числа образуют арифметическую прогрессию?

Последовательность чисел определяется как арифметическая прогрессия, только когда каждый её член (кроме первого) является средним арифметическим предшествующего и следующего членов.

Чем отличаются арифметическая и геометрическая прогрессии?

Если числовая последовательность имеет общую разность, она является арифметической; если имеет общее соотношение – геометрической.

Вывод

Арифметическая прогрессия – это числовой ряд, состоящий из последовательных членов, имеющих общую разность между членами как постоянное значение. Он используется для обобщения набора закономерностей, которые мы наблюдаем в повседневной жизни.