Теорема синусов, теорема косинусов

Теорема синусов и теорема косинусов - это два важных математических инструмента, используемых для решения треугольников и нахождения неизвестных сторон и углов в треугольниках. В этой статье мы рассмотрим основные принципы этих теорем, их формулировки и применение в практических задачах.

Теорема синусов

Теорема синусов утверждает, что отношение длин сторон треугольника к синусам соответствующих углов одинаково для всех сторон треугольника. Формально, если в треугольнике с углами A, B, и C и сторонами  a, b, и c соответственно, теорема синусов выражается следующим образом:

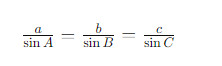
Эта теорема может быть использована для нахождения неизвестных сторон или углов в треугольнике, если известны значения одной стороны и двух углов или двух сторон и одного угла.

Теорема косинусов

Теорема косинусов утверждает, что квадрат длины любой стороны треугольника равен сумме квадратов длин остальных двух сторон минус удвоенного произведения этих сторон на косинус угла между ними. Формально, для треугольника с углами A, B, и C и сторонами  a, b, и c соответственно, теорема косинусов выражается следующим образом:

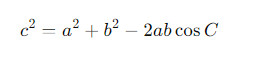
Аналогичные уравнения можно написать для других сторон треугольника.

Применение теорем синусов и косинусов

Нахождение сторон треугольника: Обе теоремы могут использоваться для нахождения длин сторон треугольника, если известны значения углов или сторон.

Вычисление углов треугольника: Теорема синусов может быть использована для вычисления значений углов треугольника, если известны длины сторон.

Решение задач геометрии: Теоремы синусов и косинусов широко применяются в задачах геометрии и тригонометрии, связанных с треугольниками, как в школьных учебниках, так и в реальной жизни, например, в навигации и строительстве.

Теорема синусов и теорема косинусов являются важными инструментами в геометрии и тригонометрии, позволяющими решать разнообразные задачи, связанные с треугольниками. Их понимание и применение имеют ключевое значение для успешного решения задач по математике и практических применений в различных областях.