Синус, косинус и тангенс угла
Синус, косинус, тангенс угла — это важные понятия в тригонометрии. Без них невозможно продолжить изучение геометрии, решать задачи. Эти понятия являются базовыми основами в тригонометри. Давайте разберем их, узнаем, что они означают, зачем нужны и как решать задачи с применением этих понятий.
Определения тригонометрических понятий
Прямой угол у нас всегда равен 90 градусов. Давайте узнаем, чему равны синус, косинус, тангенс и котангенс острого угла.
- синус острого угла — это отношение противолежащего (дальнего) катета к гипотенузе;
- косинус острого угла — это отношение прилежащего (близкого) катета к гипотенузе;
- тангенс острого угла — это отношение противолежащего (дальнего) катета к прилежащему (близкому). При вычислении его по формуле косинус не должен быть равен 0;
- котангенс острого угла — это отношение прилежащего (близкого) катета к противолежащему (дальнему). При вычислении его по формуле синус не должен быть равен нулю.
В геометрии эти понятия записываются сокращенно на латинском языке, как:
- sin;
- cos;
- tg;
- ctg.
Рассмотрим применение этих понятий на прямоугольном треугольнике.
Синус и косинус обычно представляют через экспоненциальную функцию. Теперь давайте посмотрим на прямоугольный треугольник.
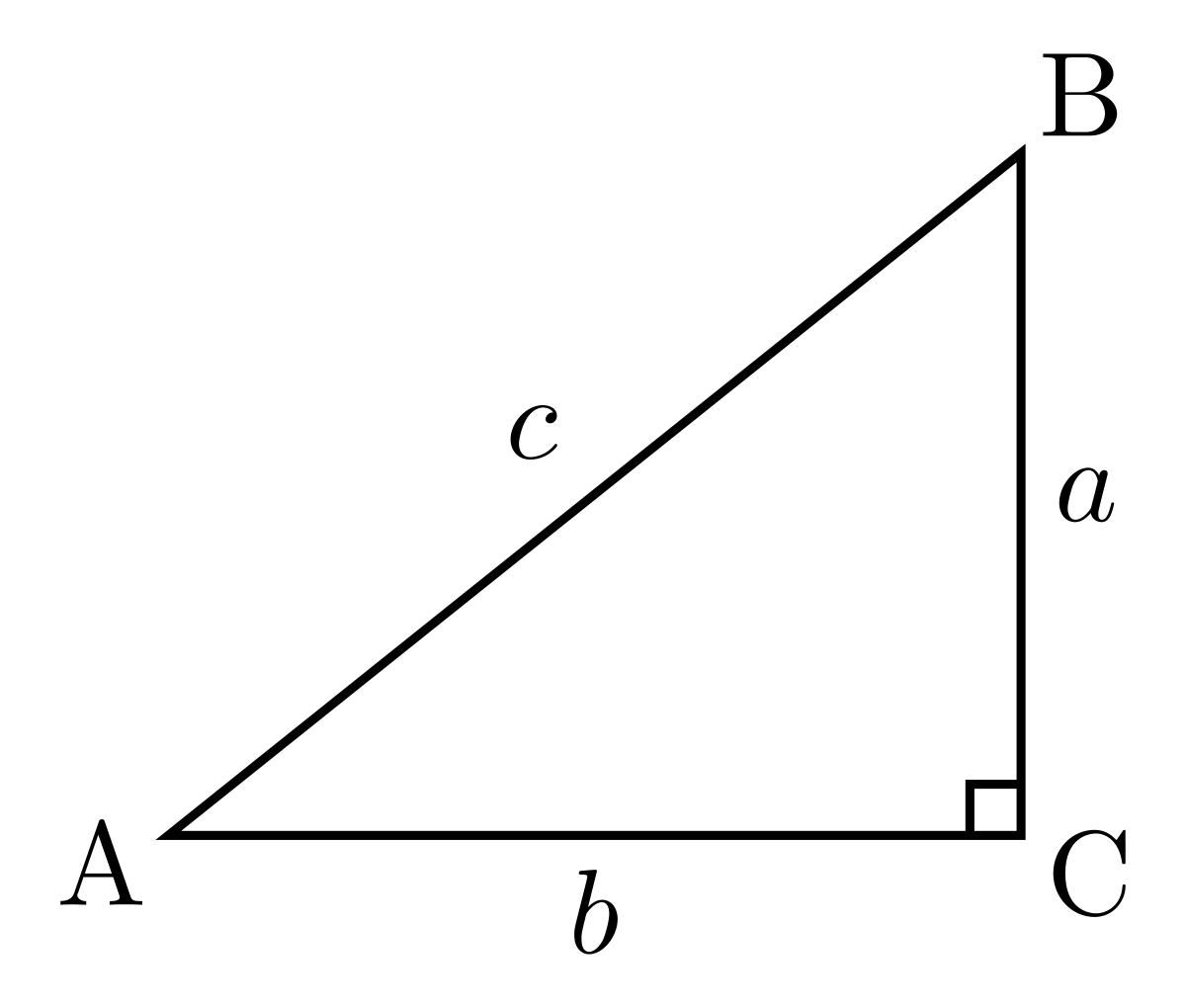
Треугольник АВС с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB. По длинам сторон треугольника мы можем найти значения функций синуса, косинуса и тангенса.
Давайте попробуем найти синус угла а. Для этого воспользуемся формулой как на скрине.

А теперь попробуем найти косинус того уже угла а. Для проведения этого решения нам нужно знать значения прилежащего катета и гипотенузы.

Теперь попробуем найти тангенс. На картинке мы имеем треугольник прямоугольный, значит тангенс будем вычислять при помощи значений противоположного катета и прилежащего по такой формуле.

Если мы говорим о числах, тупых, развернутых углов и углов, превышающих 360 градусов, то тангенс определяется при помощи синуса и косинуса (посредством их отношения и деления).
Свойства тригонометрических функций
Из определения синуса и косинуса мы понимаем, что они всегда меньше единицы. То есть область значений синуса и косинуса лежит между -1 и 1. Областью значений tg и ctg является вся числовая прямая. Эти функции могут принимать любые значения.
Функции тангенса и котангенса взаимно обратны.
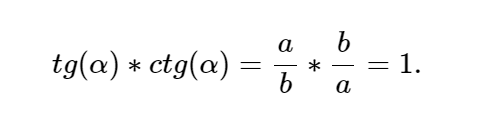
Исходя из примеров в прошлом блоке статьи и из свойств тригонометрических функций, мы подобрались к главному тригонометрическому тождеству. Мы получили его, благодаря выводу из определений синуса и косинуса с использованием теоремы Пифагора. Она звучит так: квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: c2=a2+b2.
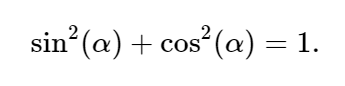
А теперь для вашего удобства мы собрали все формулы воедино в одном скрине. Изучите их и запоминайте. Так как с основными тригонометрическими формулами вы будете сталкиваться в 9, 10 классе.
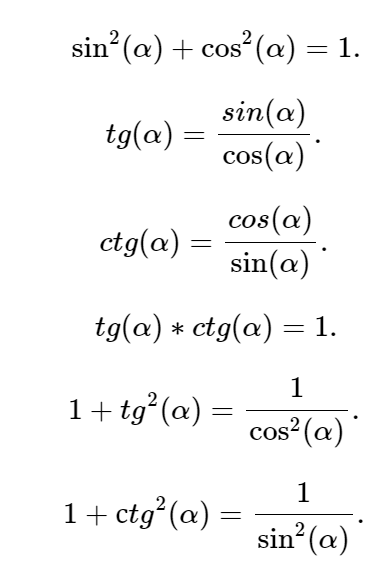
Примеры и решения задач
Зная эти формулы давайте попробуем решить одну задачу на закрепление темы.
Дан прямоугольный треугольник с острым углом. Нам нужно найти синус, косинус и тангенс острого угла.
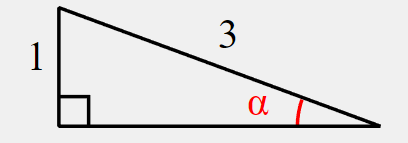
Находим прилежащий катет по теореме Пифагора, как на скрине.
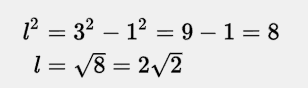
Соответственно синус, косинус и тангенс находятся по следующей формуле.
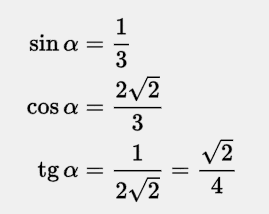
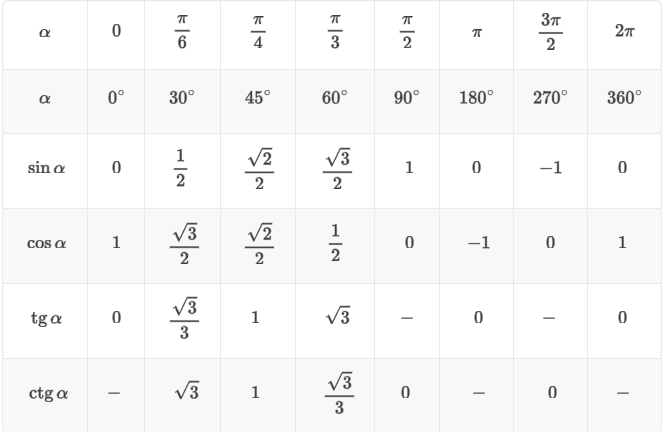
Таблица с готовыми значения синуса, косинуса, тангенса и котангенса
Следующая таблица показывает значения синуса, косинуса, тангенса и котангенса для самых используемых углов в тригонометрии.
FAQ
Что такое тригонометрия и в каких классах она изучается?
Тригонометрия — раздел математики, где изучаются тригонометрические функции. Ученые изучают их использование в геометрии. Тригонометрия появилась в 1595 г. Немецкий математик Бартоломеус Питискус, проживавший с 1561 по 1613, так назвал собственную книгу. Сама наука родилась ещё в глубокой древности и использовалась для расчётов в астрономии, архитектуре и геодезии.
Где используется тригонометрия?
Тригонометрические вычисления используют во всех областях геометрии, физики и инженерного дела. Эти функции помогают вычислять расстояния до близких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.
Вывод
Вы узнали, что такое тригонометрия и тригонометрические функции, познакомились косинусами, синусами, тангенсами и котангенсами. Запомните эти формулы, либо скопируйте их. Они помогут вам решать многие задачи по тригонометрии.
