Прямоугольные треугольники
Прямоугольные треугольники имеют прикладное значение в различных разделах математики. Например, тригонометрия исследует исключительно их свойства, а знаменитая теорема Пифагора определяет взаимосвязь между их сторонами, что находит применение в решении множества практических задач. Но не смотря на свою многогранность, свойства прямоугольных треугольников просты и понятны.
Прямоугольный треугольник – что это, определение
Прямоугольный треугольник – это треугольник, в котором один из внутренних углов прямой (равен 90°).
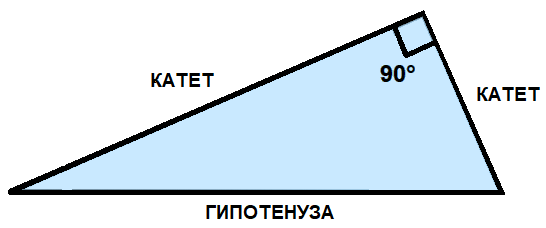
Прямой угол треугольника образован катетами (прилежащими сторонами), напротив него лежит гипотенуза (противолежащая сторона).
Свойства прямоугольного треугольника
Прямоугольные треугольники обладают множеством характеристик. На практике чаще приходится решать задачи, которые учитывают следующие свойства этой фигуры:
- сумма острых углов треугольника всегда составляет 90°;
- гипотенуза является наибольшей стороной;
- 2 высоты совпадают с его катетами треугольника;
- если опустить перпендикуляр из прямого угла на гипотенузу, то получим 3 подобных треугольника;
- если опустить медиану из прямого угла на гипотенузу, то она будет равна радиусу описанной окружности прямоугольного треугольника;
- если провести описанную окружность, проходящую через все три вершины прямоугольного треугольника, то радиус этой окружности равен половине длины гипотенузы;
- площадь прямоугольного треугольника равна половине произведения смежных сторон прямого угла.
Теорема Пифагора
В любом прямоугольном треугольнике взаимосвязь между сторонами отражена в теореме Пифагора и является фундаментальным соотношением в евклидовой (элементарной) геометрии. Теорема гласит, что сумма квадратов катетов равна квадрату гипотенузы.
Теорема Пифагора выражается простой алгебраической формулой: a2 + b2 = с2, где стороны a и b являются катетами, c – гипотенузой.
Специальные прямоугольные треугольники
Существуют специальные прямоугольные треугольники, обладающие некоторыми регулярными особенностями. Зная о них, можно упростить вычисления или вывести простые математические формулы.
Тип прямоугольного треугольника | Описание | Формула |
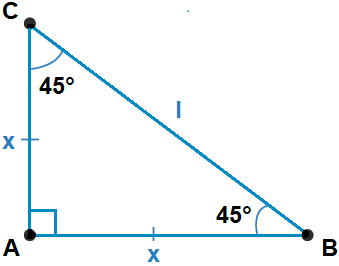
Треугольник 45-45-90 (равнобедренный) |
Равнобедренный прямоугольный треугольник – это треугольник, катеты которого равны. Теорема гласит, что в прямоугольном треугольнике 45-45-90 гипотенуза в √2 раза больше любого из катетов. | I = x√2 Поскольку катеты AB = AC = x, то по теореме Пифагора I2 = x2 + x2. Выразив гипотенузу, получаем: I = x√2. |
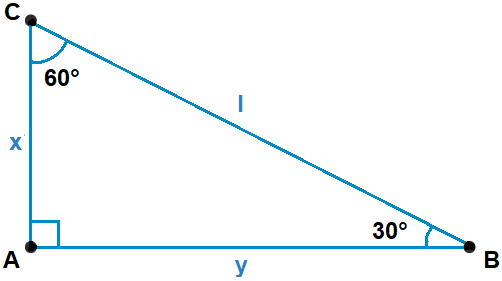
Треугольник 30-60-90 |
Теорема гласит, что в прямоугольном треугольнике 30-60-90 гипотенуза в 2 раза больше меньшего катета, а больший катет в √3 раза больше меньшего катета. | I = 2x, или x = Прямоугольный треугольник 30-60-90 составляет половину равностороннего треугольника, в котором каждый угол равен 60°. Соответственно, его короткий катет равен половине любой из сторон равностороннего треугольника, а значит, равен и половине своей гипотенузы. |
Признаки равенства
Чтобы глубоко понимать свойства 2-мерных фигур и геометрические отношения между ними, важно научиться обнаруживать сходства и различия между ними.
Признаки равенства прямоугольных треугольников немного отличаются от общих признаков равенства треугольников, т.к. образованные их катетами углы неизменно прямые (равны 90°). Известно, что 2 прямоугольные треугольники равны, если:
- катеты первого треугольника равны соответствующим катетам второго треугольника;
- любой из катетов и прилежащий к нему острый угол первого треугольника равен соответствующему катету и прилежащему к нему острому углу второго треугольника;
- гипотенуза и любой острый угол первого треугольника равен гипотенузе и соответствующему острому углу второго треугольника;
- гипотенуза и любой из катетов первого треугольника равны гипотенузе и соответствующему катету второго треугольника.
Разберем примеры – задачи и решение
На практике приходится решать разные задачи, в которых учитываются свойства прямоугольных треугольников. Чаще они требуют знания теоремы Пифагора, а также теорем, применимых к специальным треугольникам, включая фигуры 45-45-90 и 30-60-90.
Задача №1. Теорема Пифагора
Катеты AB и BC прямоугольного треугольника равны 25 и 15 соответственно. Чему равна гипотенуза AC?
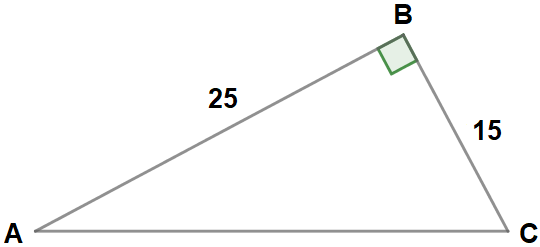
Решение:
- Согласно теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы, что выражается алгебраической формулой: AB2 + BC2 = AC2. Сразу можно вычислить величину гипотенузы прямоугольного треугольника: AC = √AB2 + BC2 = √252 + 152 = √850 = 29,15.
Ответ: 29,15.
Задача №2. Свойства прямоугольных треугольников
Величина одного из острых углов прямоугольного треугольника равна 30°, а общая сумма меньшего катета и гипотенуза – 15. Чему равна гипотенуза?
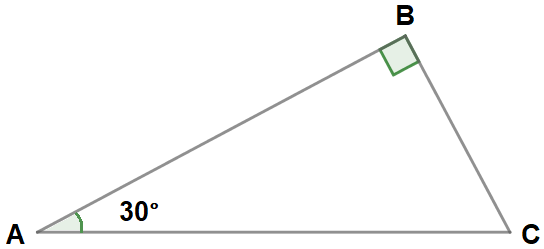
Решение:
- Сначала найдём величину неизвестного острого угла. Поскольку сумма острых углов в прямоугольном треугольнике составляет 90°, то ∠BCA = 90° – ∠BAC = 90° – 30° = 60°.
- Согласно одному из свойств прямоугольных треугольников следует: катет BC равен половине гипотенузы AC, поскольку он противолежит ∠AC в 30°. Условимся, что длина катета BC = a, в таком случае длина гипотенузы AC = 2a. Согласно условию задачи a + 2a = 15. Теперь найдём длину меньшего катета и гипотенузы: BC = a = = 5 ⇒ AC = 2a = 2 x 5 = 10.
Ответ: 10.
FAQ
Что такое катет?
Прежде чем ответить на вопрос, что такое катет, следует взглянуть на его этимологическое значение. Его корень происходит от греческого слова káthetos, что переводится как «перпендикуляр». И поэтому катетом называют любую из сторон прямоугольного треугольника, которая прилегает к прямому углу.
Какую сторону прямоугольного треугольника называют гипотенузой?
Слово «гипотенуза» имеет греческий корень, который в переводе означает «протянутая», «натянутая снизу». Гипотенуза – это сторона прямоугольного треугольника, которая расположена напротив прямого угла и соединяет катеты.
Почему в прямоугольном треугольнике гипотенуза – всегда наибольшая сторона?
Согласно теореме о соотношении углов и сторон в треугольнике, напротив большего угла лежит большая сторона. Поскольку гипотенуза всегда лежит напротив угла в 90°, то является самой длинной стороной прямоугольного треугольника.
Вывод
На первый взгляд прямоугольный треугольник – простая фигура, в которой легко идентифицировать и понять геометрические соотношения. Однако он обладает огромным количеством свойств, применяемых в различных областях математики. Чтобы уметь использовать их, нужно решать больше практических задач.