Перпендикулярность прямой и плоскости

Признак перпендикулярности прямой и плоскости изучают в 10 классе общеобразовательной школы. Он позволяет более глубоко понять взаимоотношения между этими двумя геометрическими объектами и расширить наши знания о том, как они взаимодействуют друг с другом в трехмерном пространстве.

Читайте, что такое перпендикулярность прямых и плоскостей, теоремы, формулы приведем примеры и решения задач на эту тему.

Перпендикулярность прямой и плоскости – теоремы

Перпендикулярные прямые в пространстве

Теорема является одним из фундаментальных положений геометрии, которое заключает в себе важное свойство перпендикулярности пересекающихся прямых в трехмерном пространстве.

Перпендикулярные прямые – это две прямые, которые пересекаются под прямым углом, то есть угол между ними составляет 90 градусов.

Перпендикулярность прямой и плоскости

Теорема устанавливает связь между прямой и плоскостью, определяя условия, при которых прямая перпендикулярна к плоскости.

Пусть у нас имеется плоскость П и прямая а, лежащая в этой плоскости. Тогда прямая а будет перпендикулярна плоскости П, если и только если она перпендикулярна к любой прямой, лежащей в этой плоскости и проходящей через точку пересечения прямой а с ней.

Доказательство этой теоремы основывается на определении перпендикулярности. Для двух объектов, прямой и плоскости, быть перпендикулярными означает, что угол между ними равен 90 градусов, или, что эквивалентно, их направляющие векторы ортогональны друг другу.

Если прямая а является перпендикулярной плоскости П, то она будет перпендикулярна к любой прямой, лежащей в этой плоскости и проходящей через точку пересечения прямой а с ней.

Обратная теорема: если прямая перпендикулярна различным плоскостям, то данные плоскости параллельны друг другу.

Две прямые перпендикулярные одной и той же плоскости параллельны друг другу.

Теорема позволяет установить взаимосвязь между перпендикулярностью и параллельностью прямых в трехмерном пространстве.

Две прямые, перпендикулярные одной и той же плоскости, все равно параллельны между собой.

Теорема, утверждающая, что через любую точку пространства можно провести только одну прямую, перпендикулярную к данной плоскости

Для любой точки вне данной плоскости можно провести только одну прямую, перпендикулярную к ней. Важно отметить, что эта прямая будет пересекать плоскость ровно в одной точке.

Разберем примеры – задачи и решения

Задача №1

Дано:

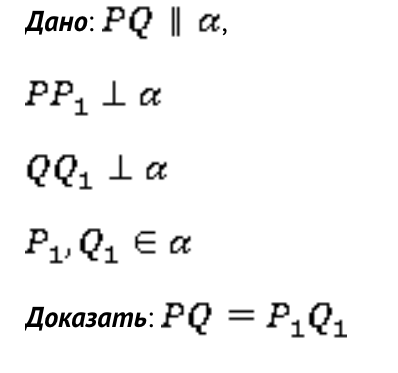
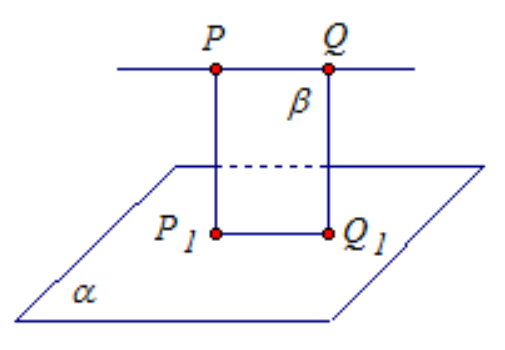
Доказательство:

1. Прямые РР1 и QQ1 параллельны, т. к. они перпендикулярны к плоскости α.
2. Пусть через них проходит плоскость β. В плоскости β прямые PQ и P1Q1 параллельны, так как по условию PQ параллельна α.
3. Выделяем прямоугольник РР1Q1Q.
4. В прямоугольнике РР1Q1Q противоположные стороны равны.
5. Получается PQ = P1Q1

Задача №2

Дано:

Треугольник ABC. С = 90, AC = 6 см, BC = 8 см, СМ – медиана.

Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК = 12 см.

Надо найти КМ.

Решение:

• Поскольку КС^ пл. АВС, значит КС^СМ.
• Треугольник КМС прямоугольный.
• МК²=СК²+МС²=144+ МС
• АВ=Ö64+36=10.
• ВМ=5.
• cosÐВ=ВС/АВ=8/10=4/5.
• Треугольник МВС, теорема косинусов:
• СМ²=ВС²+ВМ²-2 * ВС * ВМ * cosÐВ= 65 + 25 – 2 * 8 * 5 * 4/5 = 25.
• МК² = 144 + 25 = 169.
• МК = 13

Ответ: 13

Задача №3

Дано:

Треугольник ABC.

Ð А + Ð В = 90⁰.

Прямая ВD перпендикулярна к плоскости АВС.

Доказать: CD ^ AC.

Решение:

• Поскольку Ð А + Ð В = 90⁰, Ð С =90⁰.
• АС ^ ВD, АС ^ ВС, по признаку перпендикулярности прямой к плоскости АС ^ плоскости ВDС.
• По определению CD ^
• Что и требовалось доказать.

FAQ

В чем заключается признак перпендикулярности прямой и плоскости?

Признаку перпендикулярности прямой и плоскости соответствует следующее утверждение: если прямая перпендикулярна к двум пересекающимся прямым, лежащим в одной плоскости, то она перпендикулярна к этой плоскости.

Как обозначается перпендикулярность?

Перпендикулярность обозначается знаком «⊥», например, запись прямая a перпендикулярна прямой b будет в следующем виде: a ⊥ b.

Определение перпендикулярности?

Перпендикулярные прямые – это прямые, которые пересекаются друг с другом под углом 90 градусов.

Вывод

Основным фактором, определяющим перпендикулярность, является угол, образованный между прямой и плоскостью.

Перпендикулярность характеризуется тем, что этот угол составляет 90 градусов, что делает эти объекты взаимно ортогональными.

Изучение перпендикулярности дает возможность определить, насколько близки или далеки друг от друга эти объекты.