Основные понятия геометрии, 9 класс
Основные понятия геометрии за 9 класс являются фундаментальными при подготовке к ОГЭ и ЕГЭ. Рассказали основные темы с примерами, чтобы помочь разобраться в трудных и важных вопросах: как найти радиус окружности, определить уравнение окружности и прямой, длина окружности и площадь круга и др.
Уравнение окружности
Все точки окружности расположены на одинаковом расстоянии от центра окружности. Такое расстояние равно радиусу круга. Разберем, как найти r и расстояние между двумя точками.
Рассчитать расстояние между двумя точками допустимо, если установлены координаты точек:
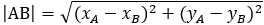 , тогда квадрат расстояния
, тогда квадрат расстояния 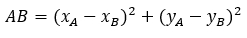
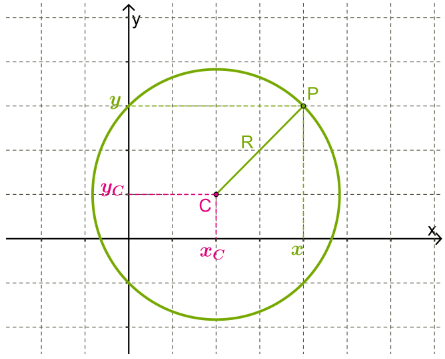
Представим, что центр окружности расположен в точке с координатами  , а радиус равен R. Любая точка P(x;y) на окружности от центра C находится на расстоянии, равном радиусу (R). Таким образом, справедливо равенство, которое одновременно является уравнением окружности:
, а радиус равен R. Любая точка P(x;y) на окружности от центра C находится на расстоянии, равном радиусу (R). Таким образом, справедливо равенство, которое одновременно является уравнением окружности:
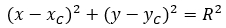
Координаты всех точек на окружности всегда удовлетворяют уравнению.
Если центр окружности будет расположен в начале координат (0;0), то уравнение окружности будет иметь вид:
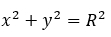
Уравнение прямой
Для составления уравнения прямой изобразим такую прямую, как перпендикуляр к некоторому отрезку с данными координатами конечных точек отрезка. Все точки перпендикуляра находятся на одинаковом расстоянии от концов отрезка.
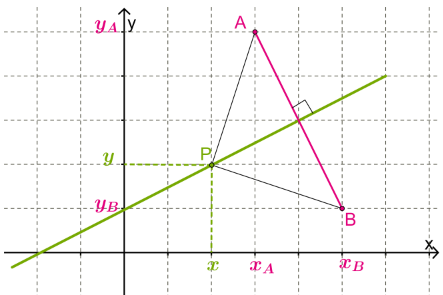
Концы отрезка имеют координаты 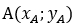 и
и 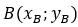 . Любая точка P(x;y) находится на одинаковом расстоянии от конечных точек PA = PB. Таким образом, если расстояния одинаковые, то и квадраты таких расстояний равны
. Любая точка P(x;y) находится на одинаковом расстоянии от конечных точек PA = PB. Таким образом, если расстояния одинаковые, то и квадраты таких расстояний равны 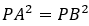 .
.
Справедливым будет равенство, которое будет являться уравнение прямой:
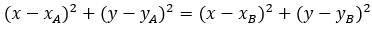
Решим составленное уравнение:
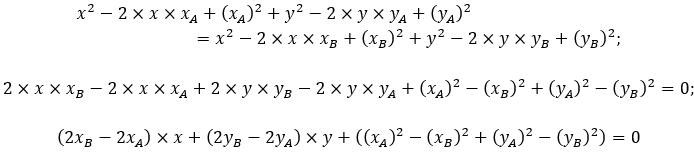
Уравнение будет в таком виде:
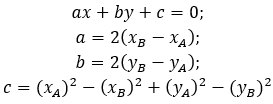
Представим, что прямая проходит через случайную точку 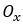 с координатами
с координатами 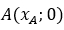 . Для любой точки на прямой
. Для любой точки на прямой 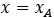 , что и будет являться уравнением прямой.
, что и будет являться уравнением прямой.
Так как ось  пересекает начало координат, то уравнение оси x = 0.
пересекает начало координат, то уравнение оси x = 0.
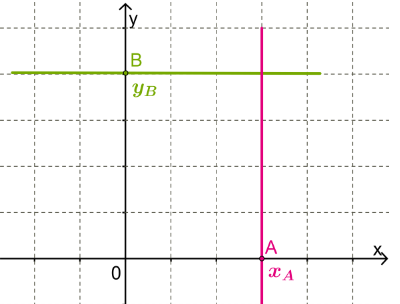
Если прямая проходит через точку на оси  с координатами
с координатами  . Для любой точки на прямой уравнение будет
. Для любой точки на прямой уравнение будет 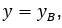 . Так как ось
. Так как ось 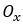 пересекает начало координат, то уравнение оси
пересекает начало координат, то уравнение оси 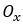 есть y = 0.
есть y = 0.
Координаты середины отрезка
Если есть координаты конечных точек отрезка, то знания о действиях с векторами и их координатами помогут определить координаты точки отрезка, расположенной посередине.
Изобразим отрезок AB на системе координат.
Конечные точки отрезка 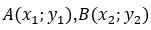 – конечные точки отрезка с данными координатами, а серединная точка имеет координаты C(x;y).
– конечные точки отрезка с данными координатами, а серединная точка имеет координаты C(x;y).
Если векторы 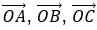 , начинаются в начале координат, то их координаты совпадут с координатами конечных точек.
, начинаются в начале координат, то их координаты совпадут с координатами конечных точек.
Если сосчитать векторы 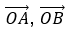 , по закону параллелограмма
, по закону параллелограмма 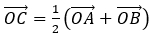 .
.
На оси координат координаты суммы определяют как сумму координат слагаемых векторов, а при умножении с числом координаты находим умножением координат.
Следовательно, 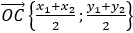 , а значит, искомые значения x и y:
, а значит, искомые значения x и y:
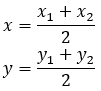
Длина окружности и площадь круга
Для всех окружностей действует правило, что отношение длины окружности и диаметру одно и то же число, которое обозначают 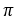 = 3,141592…
= 3,141592…
Длина окружности C, диаметр и радиус D = 2R. Таким образом, 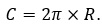
Следовательно, длина всей окружности 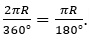
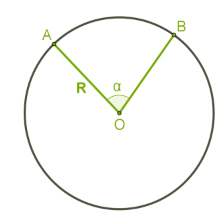
Если градусная сера дуги, образованной отрезками равна α, то длина дуги 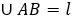 , где
, где 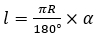
Площадь круга рассчитывается по формуле 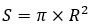 .
.
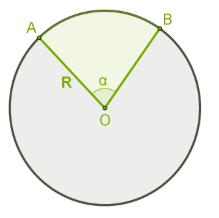
Площадь сектора, мера дуги которого 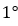 , равна
, равна 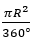 , если мера дуги равна α площадь сектора рассчитывается по площади
, если мера дуги равна α площадь сектора рассчитывается по площади 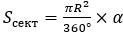 .
.
Правильные многоугольники
Многоугольники, у которых все стороны и углы равны называются правильными.
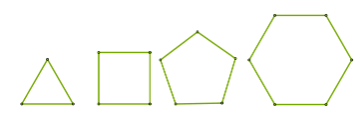
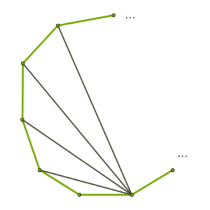
На рисунке изображены примеры правильных многоугольников.
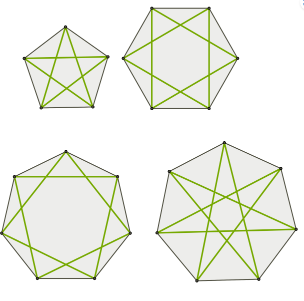
В правильных многоугольниках можно провести диагонали, которые образуют вогнутые многоугольники. Диагонали пятиугольника образуют пентаграмму, а шестиугольника – гексаграмма, семиугольника – две гептаграммы.
Если отобразить диагонали из одной вершины, любой 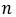 – угольник поделить на
– угольник поделить на 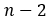 треугольника, получается сумма всех внутренних углов определяется по формуле
треугольника, получается сумма всех внутренних углов определяется по формуле 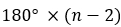 .
.
Все углы правильного -угольника одинаковые, а величина внутреннего угла равна 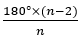 .
.
Любой правильный многоугольник можно вписать в окружность, при этом центры окружностей совпадают и такую точку называют центром многоугольника.
Вписанная окружность будет касаться всех сторон многоугольника и проходить через все вершины.
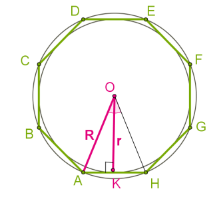
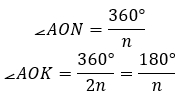
Обозначим AH = a.
В треугольнике 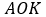 связаны стороны AK (50% от AH), радиус описанной окружности
связаны стороны AK (50% от AH), радиус описанной окружности 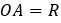 и радиус вписанной окружности
и радиус вписанной окружности 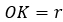 .
.
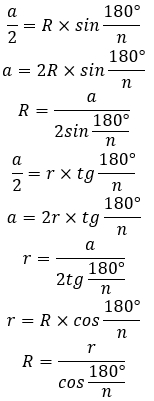
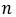 – угольник состоит из
– угольник состоит из 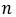 треугольников, равных
треугольников, равных 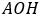 , а значит верна формула:
, а значит верна формула:
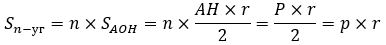
FAQ
Какие задания могут встретиться на ЕГЭ по геометрии?
Список заданий за предыдущие годы с ответами и описанием ошибок, которые допустили ученики, представлен на сайте ФИПИ. Нельзя с уверенностью сказать, что при сдаче придется определять радиус окружности или площадь правильного многоугольника, однако данные знания являются базовыми при изучении геометрии за 9 класс. Их глубокое понимание позволит применить формулы для получения промежуточного результата в тесте или сориентироваться в решении задач по другим темам.
Для чего нужно знать уравнение окружности?
Уравнение окружности необходимо чтобы найти ее центр и радиус.
Рассмотрим на примере: из двух уравнение нужно определить какое из них является уравнением окружности
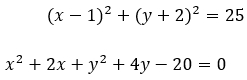
Уравнением окружности является 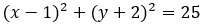 . Значит центр окружности — точка с координатами Q (1; -2), а r окружности
. Значит центр окружности — точка с координатами Q (1; -2), а r окружности 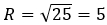 .
.
Второе уравнение тоже можно преобразовать в уравнение окружности:
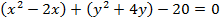
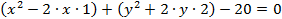
Так как в каждой скобке есть квадрат одного выражения и произведение с множителем на 2, нужно определить квадрат второго выражения, затем найти его сумму и разность:
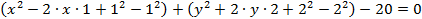
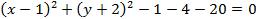
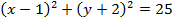
В школьную программу включают много геометрического материала не только при изучении профильного предмета, но и в начальный курс по математике. Такие изменения были необходимы, чтобы учитель мог познакомить учеников с геометрическими фигурами. их свойствами и особенностями им нужна соответствующая математическая подготовка. В дальнейшем любые вопросы могут быть задачами на экзамене. И если сейчас решить задачи на рассмотренные темы можно на онлайн-тренажерах или специальных калькуляторах, то использование «помощников» при сдаче ОГЭ или ЕГЭ запрещены. В качестве тренажера или для проверки решения использовать онлайн-ресурсы можно, поэтому добивайтесь понимания тем при их изучении в школе, чтобы в будущем не тратить много времени и сил на подготовку.
