Объем прямоугольного параллелепипеда

Большинство предметов, которые нас окружают – это параллелепипеды. Находить их объем важно не только для решения уроков по математике, но и для вычисления материала при стройке или количестве необходимой жидкости в аквариуме.

В этой статье мы расскажем, что такое прямоугольный параллелепипед, как найти его объем, в каких единицах он измеряется, а также решим несколько примеров по теме.

Основные понятия

Параллелепипед – это геометрическое тело с 6 гранями, каждая из которых является прямоугольником. Грани этого фигурного объекта соответствуют парам параллельных прямых, и поэтому он получил такое название.

Прямоугольный параллелепипед – это параллелепипед, у которого 4 боковые грани и основание являются прямоугольниками.

На рисунке изображен прямоугольный параллелепипед

Грани – прямоугольники, из которых состоит прямоугольный параллелепипед. Всего граней в параллелепипеде 6.

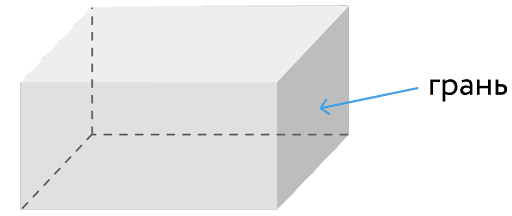
Ребра – это стороны граней прямоугольного параллелепипеда. У каждого прямоугольного параллелепипеда есть 12 ребер.

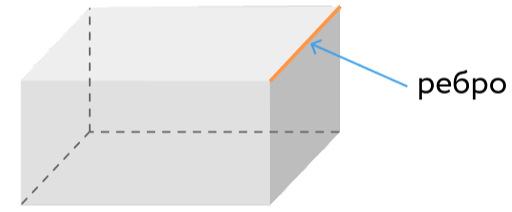
Вершина – общая точка трёх граней (длины ребер) прямоугольного параллелепипеда. Всего в прямоугольном параллелепипеде 8 вершин.

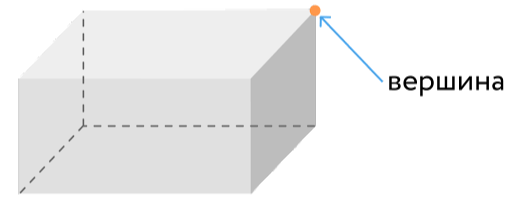
Объем параллелепипеда можно определить как произведение трех его сторон – длины, ширины и высоты. Это основная характеристика, которая позволяет определить, сколько пространства занимает данный геометрический объект.

Объем прямоугольного параллелепипеда

Объем прямоугольных параллелепипедов – это объем пространства, занимаемого этим геометрическим телом. Для нахождения объема необходимо знать его длину (a), ширину (b) и высоту (h).

Формула для расчета объема прямоугольного параллелепипеда выглядит следующим образом:

V = a * b * h, где V – объем, а и b – соответствующие стороны, h – высота параллелепипеда.

Следуя этой формуле, можно вывести, что объем прямоугольного параллелепипеда равен произведению площади его основания на высоту:

V = Sосн * h, где Sосн – площадь основания, h – высота.

Способы перевода единиц объема

Зачастую, для решения задач необходимо перевести одну единицу объема в другую, например кубические дециметры в кубические сантиметры. Есть основной принцип, который поможет освоить перевод. Рассмотрим его на следующем примере.

Найти: сколько кубических сантиметров в кубическом метре?

Решение:

Необходимо посмотреть, сколько кубиков со стороной 1 сантиметр поместится в куб со стороной 1 м.

В один ряд укладывается 100 штук (ведь в одном метре 100 см).

В один слой укладывается 100 рядов или 100 * 100 кубиков.

Всего помещается 100 слоев.

Всего 100 * 100 * 100 = 1 000 000 шт.

Таким образом, 1 м³ = 1 000 000 см ³.

То есть если линейные величины связаны соотношением «в одном метре 100 см», то чтобы получить соотношение для кубических величин, нужно возвести 100 в 3 степень (100³ = 1 000 000). И не нужно каждый раз чертить кубы.

Примеры решения задач

Решим несколько задач по поиску объема прямоугольного параллелепипеда.

Пример 1

Дано: длины трех сторон фигуры: а = 9 см., b = 13 см., h = 16 см.

Найти: площадь прямоугольного параллелепипеда.

Решение:

Подставим данные в формулу для вычисления:

V = a * b * h

V = 9 * 13 * 16

V = 1872 см³

Ответ: объем прямоугольного параллелепипеда будет равен 1872 см³.

Пример 2

Дано: холодильник имеет высоту 2 метра, ширину 60 см и глубину 50 см.

Найти: вычислить объем холодильника.

Решение

Прежде чем воспользоваться формулой объема – произведение длин всех сторон – необходимо перевести длины в одинаковые единицы измерения. Мы можем перевести все в сантиметры:

• Высота (h) 2 метра = 200 см.
• Ширина (a) 60 см.
• Глубина (b) 50 см.

Подставим данные в формулу для вычисления:

V = a * b * h

V = 60 * 50 * 200

V = 600 000 см³

Ответ: объем холодильника равен 600 000 кубическим сантиметрам.

Пример 3

Найти: сколько кубических метров в одном кубическом километре?

Решение:

1 км = 1 000 м.

1 000³ = 1 000 000 000 = 1 млрд.

1 км³ = 1 000 000 000 м ³= 1 млрд. м³.

Ответ: в одном кубическом километре 1 млрд. метров в кубе.

FAQ

В каких единицах измеряется объем прямоугольного параллелепипеда?

Объем прямоугольного параллелепипеда измеряют в кубических единицах:

• мм³ (кубический миллиметр);
• см³ (кубический сантиметр);
• дм³ (кубический дециметр);
• м³ (кубический метр).

Есть ли способы упрощения расчета объема прямоугольного параллелепипеда?

Да, чтобы ускорить процесс вычисления объемов прямоугольных параллелепипедов, можно воспользоваться онлайн калькулятором. Вот несколько самых популярных:

• OnlineMSchool – онлайн калькулятор для вычисления объема прямоугольных и наклонных параллелепипедов. Здесь вы сможете очень просто и быстро найти объем прямоугольного параллелепипеда, зная значения его длины, ширины и высоты.
• Calc.by – онлайн калькулятор для расчета объема прямоугольного параллелепипеда Для работы введите значение ребер a, b, c и нажмите кнопку «Рассчитать». Также вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
• Ecalc – калькулятор расчета объема прямоугольного параллелепипеда. Здесь можно не только рассчитать площадь, но и изучить теоретическую часть, например, как вычислить диагональ прямоугольного параллелепипеда, а также посмотреть ответы на частые вопросы по теме.

Вывод

• Прямоугольный параллелепипед – это фигура, которая окружает нас повсюду: монитор, крышка стола, аквариум, телефон и многое другое.
• Вычисление площади прямоугольного параллелепипеда – процедура несложная, если внимательно изучить теоретическую часть.
• В этой статье мы дали подробное описание такой фигуре, показали, как искать объемы прямоугольного параллелепипеда по формулам.
• Для тех, кто хочет упростить задачу с вычислением объема, мы нашли несколько популярных онлайн-калькуляторов.