Законы Ньютона

Основу классической механики заложили законы Ньютона. Они отвечают на многие вопросы, которые возникают в совершенно бытовых условиях, например, почему при резком торможении транспортного средства, его пассажиры движутся вперед? Разберемся в формулировках и применении законов Ньютона, разберем несколько примеров для закрепления.

Инерция

Законы Ньютона могут быть использованы для движения любой механической системы. Это может быть движение человека, автомобиля, робота и т.д. Вспомним про транспорт и движение вперед его пассажиров, вызванное резкой остановкой. При торможении возникает инерция – явление, при котором сохраняется постоянная скорость тела при отсутствии на него действия других тел.

Инерция возникает в различных ситуациях и ежедневно:

• если вы перестанете крутить педали, то велосипед не прекратит свое движение в течение некоторого времени;
• бегун не останавливается сразу после финиша, а движется еще некоторое время;
• кофе не останавливает свое вращение сразу после того, как вы перестали его размешивать и вытащили ложку;
• дверь захлопывается после того, как вы толкнули ее.

Явление инерции объясняется Первым законом Ньютона, который еще называется законом инерции. О нем мы поговорим дальше.

Формулировка Первого закона Ньютона

Есть такие системы отсчета, которые называются инерциальными (ИСО). В них тело находится в состоянии покоя (V=0) или движется равномерно и прямолинейно (V=const), на него не действуют силы или их действие компенсируются (F=0).

Инерциальные системы отсчета существуют везде, например, лифт, который равномерно опускается или поезд метро, который равномерно движется между станциями.

У инерциальных систем отсчета есть такие свойства:

• тела движутся равномерно или находятся в покое;
• одинаковые начальные условия обеспечивают телам одинаковое движение;
• изменение скорости тела может произойти в случае, если на него действует другое тело.

Рассмотрим последнее свойство подробнее.

Предположим, что кот Исаак лежит на батарее. Но он не просто лежит, на него действуют сразу две силы:

• сила гравитации земли (сила тяжести), которая направлена вниз;
• сила реакционной опоры со стороны батареи, которая направлена вертикально вверх.

Несмотря на то, что на кота действуют сразу две силы, он остается неподвижным, так как действие этих сил скомпенсировано.

Первый закон Ньютона не имеет формулы, но его можно математически описать следующим образом:

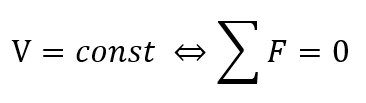
В этой формуле V – скорость тела, которая измеряется в метрах в секунду, а 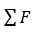 – равнодействующая сила, которая измеряется в ньютонах.

Равнодействующая сила представляет собой векторную сумму всех сил, которое действуют на тело. Если тело находится в состоянии покоя или движется равномерно прямолинейно, то равнодействующая сила равна нулю.

Формулировка Второго закона Ньютона

Пока кота Исаака никто не трогает, он находится в состоянии покоя, но если подойти и толкнуть его с некоторой силой, то его скорость изменится. От размера приложенной силы напрямую зависит ускорение, которое получит Исаак. Взаимосвязь между ускорением и приложенной силой описывается Вторым законом Ньютона.

В ИСО ускорение, с которым движется тело прямо пропорционально равнодействующей всех сил и обратно пропорционально массе тела.

Если вспомнить вагон метро, то под действием равнодействующей силы он будет получать ускорение. Чем больше равнодействующая сила, тем больше ускорение. Но, если не увеличивать равнодействующую силу, а уменьшить массу вагона, то и ускорение, которое он получит, увеличится.

Отсюда появляется формула Второго закона Ньютона:

В этой формуле a – ускорение (м/с²), F – равнодействующая сила (Н) и m – масса (кг).

Обратите внимание, что сила и ускорение являются векторными величинами, при этом их направления всегда совпадают.

Задачи с решениями на Второй закон Ньютона

Решим несколько задач на 2-й закон Ньютона, чтобы было проще усвоить материал.

Задача 1.

Если горизонтально бросить сумку массой 6 кг с силой 6 Н, то какое ускорение получит сумка? (силой сопротивления воздуха можно пренебречь).

Решение:

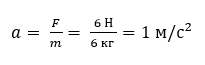
Ответ: сумка получила ускорение 1 м/с².

Задача 2.

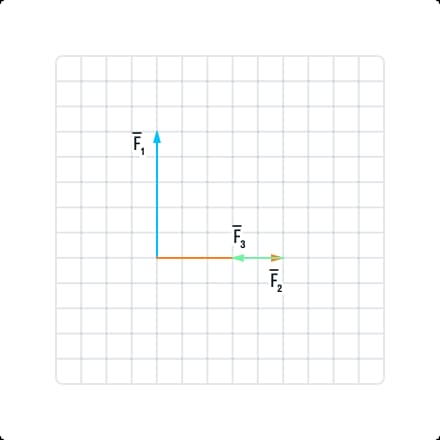
На рисунке вы видите 3 силы, которые действуют на тело. Найдите равнодействующую силу при условии, что одна клетка = 1Н.

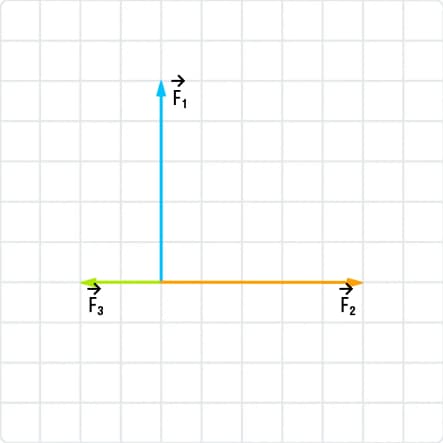
Решение:

Чтобы найти равнодействующую силу, необходимо отыскать векторную сумму всех трех сил. Для этого требуется воспользоваться правилами сложения векторов. Так как векторы F₂ и F₃ лежат в горизонтальной плоскости, но они направлены в разном направлении, то при их сложении нужно будет последовательно отложить их друг от друга. В результате получится, что сумма будет равна трем клеткам, а направление – вправо.

Далее сложим полученную сумму с силой F₁ по правилу параллелограмма. Для этого отложим силы F₁ и F₂₃ из одной точки, достроим их до параллелограмма. Диагональ полученной фигуры и станет искомой величиной .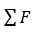

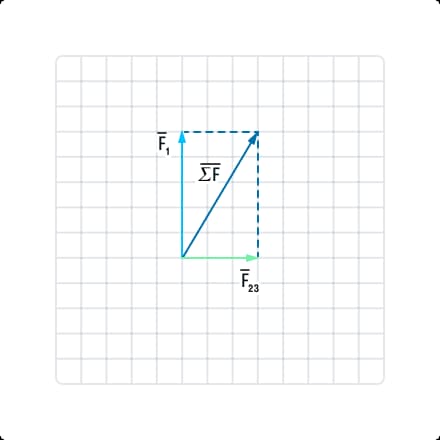
Чтобы найти ее значение, необходимо отыскать гипотенузу:

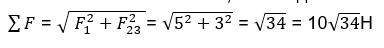
Алгоритм решения задач с применением 2-го закона Ньютона

Чтобы правильно решать задачи с использованием 2-го закона Ньютона, необходимо следовать следующему алгоритму:

1. Выбрать ИСО.
2. Отметить на рисунке все силы, которые действуют на тело.
3. Перевести 2-й закон Ньютона в векторный вид.
4. Найти проекции сил на координатные оси.
5. Выполнить запись 2-го закона Ньютона в проекциях на оси.
6. Составить и решить систему уравнений.
7. Произвести расчеты и записать ответ.

Формулировка Третьего закона Ньютона

Действие тел на друг друга осуществляется с силами, которые направлены вдоль одной прямой, но с противоположными направлениями и разными модулями. Это и есть то самое «сила действия = силе противодействия».

Мы наблюдаем это повсюду:

• люди притягиваются к Земле с той же силой, что и Земля притягивается к людям;
• груша «ударяет» боксера с той же силой, что и он ее, поэтому он надевает перчатки;
• кот Исаак давит на батарею с такой же силой, с какой и батарея на кота.

Выразить Третий закон Ньютона через формулу можно следующим образом:

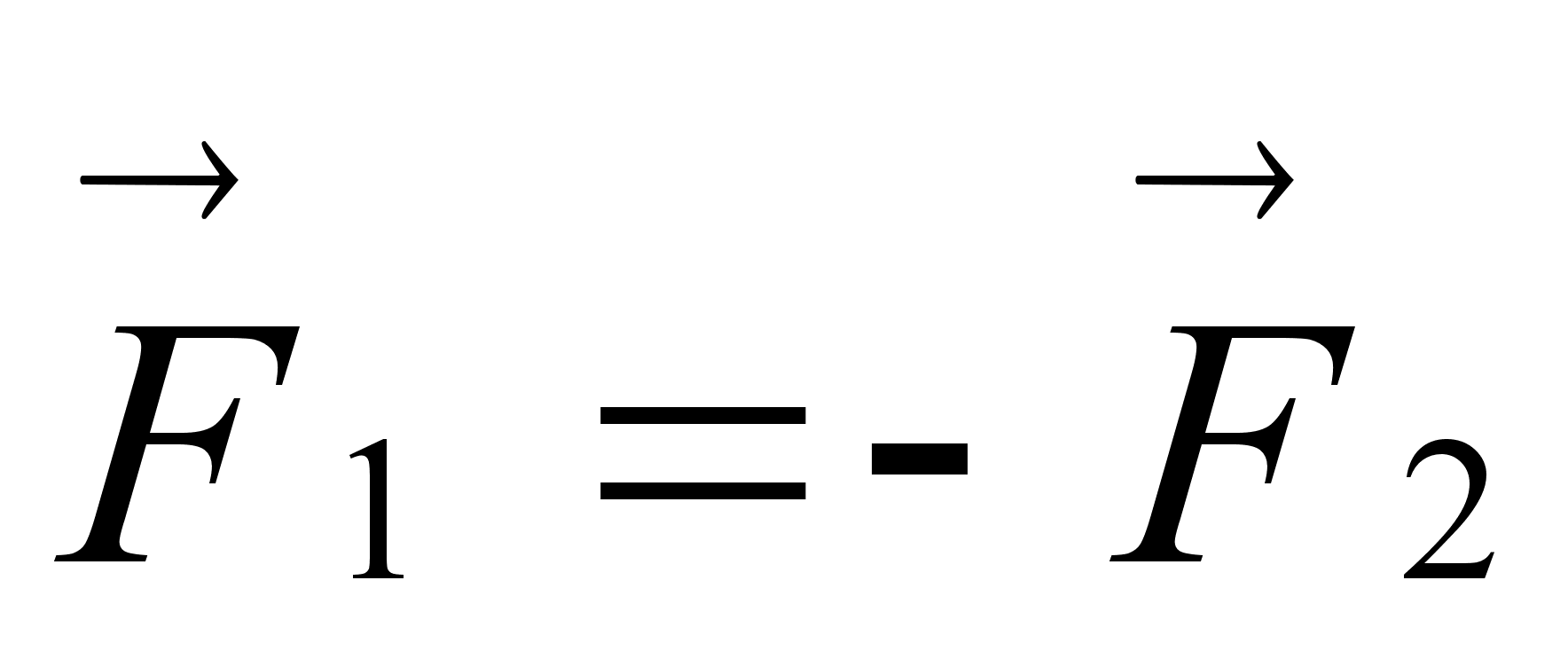
В ней F₁ – сила, с которой первое тело действует на второе (в ньютонах), а F₂ – наоборот, сила, с которой второе тело действует на первое (в ньютонах).

В задачах чаще всего используется комбинация 2-го и 3-го законов:

Рассмотрим пример задачи по Третьему закону ньютона:

Задача 3.

Во время перетягивания каната одна команда тянет его с силой 250 Н, а вторая – с неизвестной. Найдите силу, с которой вторая команда тянет канат, если обе команды в результате стоят неподвижно.

Решение:

Так как сила действия равна силе противодействия, чтобы обе команды не двигались с места, вторая команда должна тянуть канат с равной силой. Именно сила 250 Н, с которой вторая команда воздействует на канат позволит удерживать команды в неподвижном положении.

FAQ

Какие законы Ньютона применяются при решении практических задач?

Задачи чаще всего дают на Второй и Третий законы, так как в 1 законе можно задавать только вопросы, связанные с формулировкой самого закона.

Почему неподвижная система все равно является инерциальной?

Это связано с тем, что на тело, находящееся в покое все равно действуют определенные силы, однако они компенсируются друг за счет друга.

Появляются ли вопросы на законы Ньютона в ЕГЭ?

Да, вопросы для экзаменов могут попадаться как на 1, так и на 2 или 3 законы. Их понимание позволит получить дополнительные баллы, причем достаточно просто.

Вывод

Законы Ньютона позволяют описывать движения любой механической системы и становятся основами классической механики. Они пригодятся не только для получения хороших оценок в школе, но и потребуются при сдаче экзамена, если ребенок решил поступать на техническую специальность. Эти законы достаточно просты для понимания и запоминания, а минимальное количество формул позволяет достаточно быстро выучить их. Главное – больше практиковаться при решении задач, уметь визуализировать вопросы, связанные с Первым законом.