Закон Ома
При изучении электричества и связанных с ним явлений в первую очередь рассматриваются 3 фундаментальные понятия: напряжение, сила тока, сопротивление. Эти величины тесно взаимосвязаны и характеризуют поведение заряженных частиц. Зависимость между ними описывает закон Ома, глубоко понимая который, можно манипулировать и использовать электричество в своих целях.
Закон Ома – определение
Закон Ома – это фундаментальный закон в электротехнике, сформулированный в 1927 г. немецким физиком Г. Омом. Он используется при расчёте напряжения, силы тока и сопротивления в постоянных цепях.
В широком смысле закон Ома гласит, что напряжение на проводнике прямо пропорционально силе тока (току), протекающего через него. Закон верен при условии, что температура и прочие физические показатели окружающей среды постоянны.
Закона Ома для участка цепи
На практике, работая с электрическими цепями, учитывается и показатель сопротивления. В таком случае закон Ома будет сформулирован так: электрический ток на участке цепи прямо пропорционален напряжению на его концах и обратно пропорционален сопротивлению.
Закон Ома для участка цепи математически выражается формулой, которая связывает напряжение (U), ток (I) и сопротивление (R):
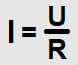
Таблица 1. Основные компоненты закона Ома
|
Понятие |
Сущность |
Символ |
Единица измерения |
|
Сила тока |
Выражает скорость потока электрических зарядов в проводнике под влиянием разности потенциалов (напряжения) |
I |
ампер (А) |
|
Напряжение |
Показывает энергию, которая потребляется или передаётся электрическими зарядами в цепи. Создаёт электрическое поле, которое инициирует движение электронов |
V |
вольт (В) |
|
Сопротивление |
Описывает способность компонента (его материала) электрической цепи препятствовать току |
R |
ом (Ом) |
Применение
Закон Ома широко используется при решении практических задач в отраслях электротехники и электроники. Его применяют в разных целях, включая:
- проектирование электрических схем;
- разработку схем управления автоматизированными механизмами;
- расчёт предельных нагрузок на источники питания;
- оценку функциональности электронных компонентов устройств;
- оценку энергопотребления устройств и безопасности электрических систем.
Таблица удельных сопротивлений разных материалов
Из закона Ома следует, что сопротивление (R) прямо пропорционально напряжению (U) и обратно пропорционально силе тока (I). Это выражается формулой:
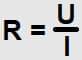
Но нужно понимать, что сопротивление не зависит от напряжения или силы тока. Напротив, во сколько раз увеличится (уменьшится) сопротивление проводника, во столько же увеличится (уменьшится) сила тока; при этом отношение между напряжением и силой тока останется прежним.
Немецкий физик Г. Ом в ходе опытов установил, что сопротивление прямо пропорционально длине (l), обратно пропорционально площади поперечного сечения (S) проводника и зависит от его материала. При этом, чтобы учесть зависимость показателя от определённого вещества, рассчитывают удельное сопротивление (ρ) – сопротивление проводника длинной 1 м и поперечным сечением 1 м2.
Тогда сопротивление выразим формулой:
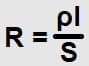
Из указанной формулы выразим удельное сопротивление и получим единицу измерения:
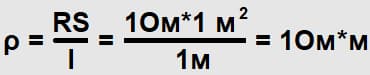
Площадь поперечного сечения принято указывать в мм2, т.к. зачастую она мала. Поэтому единицу измерения удельного сопротивления приводят в соответствующую форму:
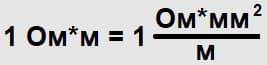
Удельное сопротивление материалов измеряют в лабораторных условиях: фиксируют напряжение и ток на проводе с определённой длиной и площадью поперечного сечения. Показатели, характеризующие различные материалы, известны и представлены в стандартных таблицах. Их можно использовать при расчёте напряжения и силы тока в постоянных цепях.
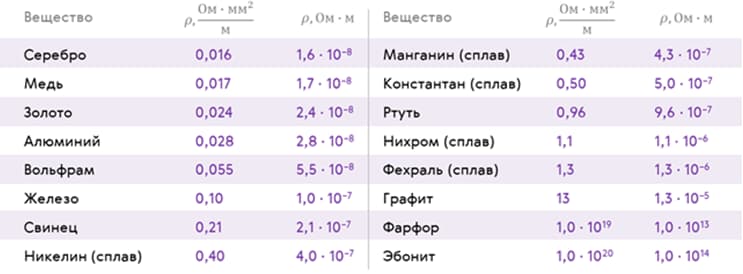
Таблица 2. Удельное электрическое сопротивление некоторых веществ (при t = +20°C)
Резистор
Поскольку отношение между напряжением, силой тока и сопротивлением в электрических цепях постоянно (подчинено закону Ома), то мы можем контролировать любую переменную, манипулируя остальными. Считается, что проще всего управлять сопротивлением: заменять основной материал, регулировать размер и форму проводящих компонентов.
Чтобы поддерживать точное значение сопротивления, в электрическую цепь включают резистор. Это пассивный компонент, который обеспечивает линейное преобразование тока в напряжение и наоборот, а также перераспределение электрической энергии.
По характеру изменения сопротивления выделяют 3 типа резисторов:
- постоянные;
- переменные регулировочные (реостаты);
- переменные подстроечные.
Технические характеристики резисторов
При выборе резистора обращают внимание на три основных параметра:
- Номинальное сопротивление. Выражает фактическое сопротивление проводника и выражается в омах (Ом), например, 1 кОм (1000 Ом), 1 МОм (1000 кОм).
- Номинальная мощность. Резисторы оцениваются с точки зрения того, сколько тепловой энергии они способны рассеивать без перегрева и повреждения. Показатель измеряется в ваттах (Вт). Большинство резисторов, используемых в схемах небольших электронных устройств, обладают номинальной мощностью 0,25 Вт и меньше.
- Класс точности (допуск). Показывает, насколько фактическая величина сопротивления может отклоняться от номинального значения. Выражается в процентах (%). Наиболее распространёнными являются резисторы с допусками 5%, 10%, 20%.
Дополнительные характеристики, которые тоже могут быть нужны: максимальное рабочее напряжение, стойкость к температурам и влаге, избыточный шум, коэффициент напряжения. Если элемент будет применяться в высокочастотном или сверхвысокочастотном оборудовании, учитывается его паразитная емкость и паразитная индуктивность. Чем меньше эти значения, тем более качественный резистор.
Обозначение на схемах
В соответствии с ГОСТ 2.728-74 условным графическим обозначением (УГО) резистора на схемах является прямоугольник размером 10*4 мм.
Таблица 3. Основные условные графические обозначения резисторов
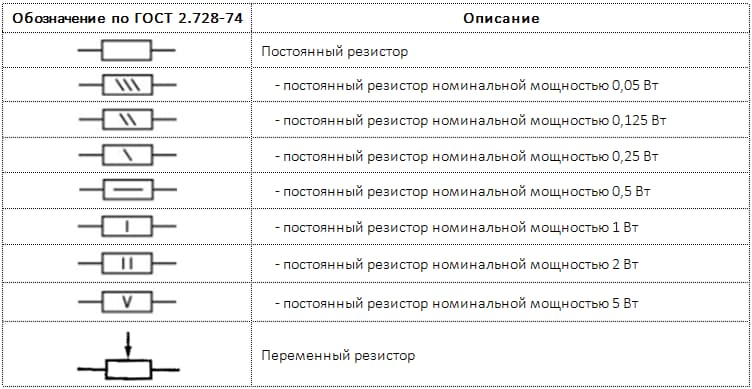
Реостат
При решении задач электротехники часто приходится меня силу тока, например, чтобы управлять громкостью радиоприёмника, скоростью электродвигателя и пр. С этой целью используют реостаты.
Реостат – это тип переменного резистора, состоящий из проводящего элемента и регулятора сопротивления. За счёт изменения показателя сопротивления он меняет силу тока.
В тексте ГОСТ 2.728-74 определены условные графические обозначения (УГО) переменных резисторов в реостатном включении.
Таблица 4. Основные условные графические обозначения реостатов
Параллельное и последовательное соединение
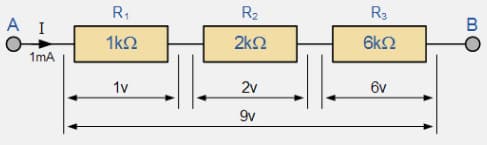
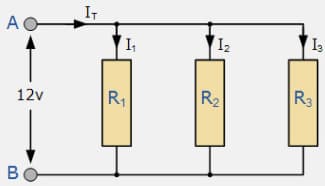
На практике компоненты электрической цепи (или электронной схемы) могут быть соединены последовательно или параллельно. В первом случае они размещены по одному пути, во втором – по нескольким путям. И в каждом из этих случаев есть свои особенности расчёта базовых показателей: напряжения, силы тока и сопротивления.
Таблица 5. Отличия последовательных и параллельных электрических цепей
|
Сравнительная характеристика |
Последовательное соединение |
Параллельное соединение |
|
Базовая схема |
|
|
|
Количество поволоки |
Нужно немного проволоки |
Нужно много проволоки |
|
Сила тока |
Сила тока одинакова по всей цепи |
Ток цепи от батареи до какого-либо компонента представляет собой сумму всех токов компонентов цепи после прохождения через неё |
|
Напряжение |
Напряжение батареи представляет собой сумму напряжений всех компонентов цепи |
Напряжение всех компонентов цепи одинаково |
|
Функциональность |
Если какой либо компонент повреждён, то остальные не работают, т.к. поток электронов прерывается |
Если какой-либо компонент повреждён, то остальные сохраняют работоспособность |
Разберем примеры – задачи и решение
Задача №1. Расчёт силы тока
В цепь включён медный проводник, на концах которого фиксируется напряжение 6,8В. Заранее известно, что его длина составляет 100 м, а площадь поперечного сечения – 0,5 мм2.
|
Дано: l = 100 м; S = 0,5 мм2; U = 6,8В; ρ = 0,017 Ом*мм2/м |
Решение: I = U / R, R = ρ ( l / S ) I = U x S / ρ x l = 6,8 x 0,017 x 100 = 2 [А] Ответ: I = 2А |
|
I = ? |
Подробное решение:
Сначала запишем краткое условие поставленной задачи (слева от вертикальной черты). Заранее нам известны: длина проволоки (l) – 100 м, площади поперечного сечения (S) – 0,5 мм2, напряжение (U) – 6,8 В. Величину удельного сопротивления меди узнаём из таблицы: ρ = 0,017 Ом*мм2/м. Под горизонтальной чертой на рис. Нужно найти силу тока (I).
Чтобы решить задачу, потребуются 2 формулы: на расчёт силы тока на участке цепи и сопротивления. Из них сформируется общее выражение: I = U x S / ρ x l. Затем подставляем в формулу известные значения и осуществляем расчёт: I = 6,8 x 0,017 x 100 = 2 [А].
Получаем ответ: сила тока на участке цепи составляет 2А.
Задача №2. Расчёт поперечного сечения проволоки
По вольфрамовой проволоке протекает ток. Её длина составляет 5 м; путём измерения были получены значения силы тока – 0,05А и напряжения – 5В. Какова площадь поперечного сечения проволоки?
|
Дано: l = 5 м; I = 0,05А; U = 5В; ρ = 0,055 Ом*мм2/м |
Решение: R = ρ ( l / S ) ⇒ S = ρ x l / R ⇒ R = ? I = U / R ⇒ R = U / I S = ρ x l x I / U = 0,055 x 5 x 0,05 / 5 = 0,00275 мм2 Ответ: S = 0,00275 мм2 |
|
S = ? |
Подробное решение:
Сначала запишем краткое условие поставленной задачи (слева от вертикальной черты). Заранее нам известны: длина проволоки (l) – 5 м, сила тока (I) – 0,05А, напряжение (U) – 5В. Показатель сопротивления вольфрама берём из таблицы: ρ = 0,055 Ом*мм2/м. Требуется найти площадь поперечного сечения (S).
Запишем формулы на расчёт сопротивления, выразим из неё площадь сечения проводника: S = ρ x l / R. Пользуясь указанной формулой, нельзя сразу найти сечение, поскольку неизвестно сопротивление. Чтобы рассчитать его, воспользуемся соответствующей формулой закона Ома для участка цепи: R = U / I. Теперь формула площади сечения изменится: S = ρ x l x I / U. Подставляем в формулу известные значения и получаем: S = 0,055 x 5 x 0,05 / 5 = 0,00275 мм2.
Получаем ответ: площадь поперечного сечения вольфрамовой проволоки составит 0,00275 мм2.
FAQ
Какова формула сопротивления, напряжения и тока?
Формула сопротивления, напряжения и тока выражается как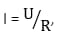 
где I – ток в амперах, U – напряжение в вольтах, а R – сопротивление в омах.
Каковы 3 формы закона Ома?
Закон Ома можно переписать в 3 различных формах в зависимости от неизвестных и заданных величин:
- напряжение равно току, умноженному на сопротивление (V = I x R);
- сопротивление прямо пропорционально напряжению, обратно пропорционально току (R = U / I);
- ток прямо пропорционален напряжению, обратно пропорционален сопротивлению (I = U / R).
Как легко запомнить варианты закона Ома?
Математическую взаимосвязь между напряжением, током, сопротивлением можно выразить с помощью треугольника Ома. В его верхней части указывается сопротивление, в нижней – ток и напряжение (последовательность нижних показателей не важна).
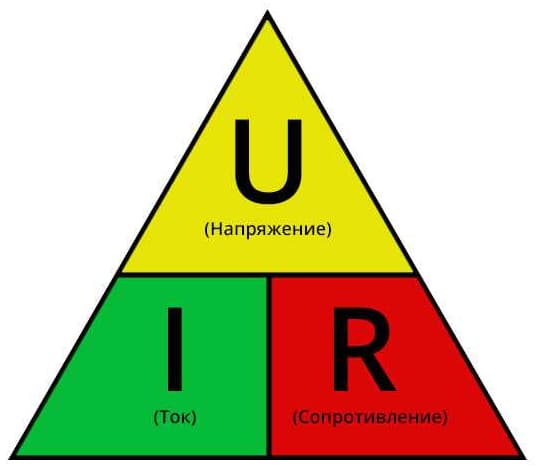
Закройте рукой неизвестную переменную. Если оставшиеся показатели расположены рядом – нужно их перемножить, в противном случае – разделить верхнюю часть на нижнюю.
Вывод
Закон Ома – это фундаментальный закон, который используется в работе с электрическими цепями. Хотя он кажется простым, ученикам 8 класса сложно сразу понять, как взаимосвязаны напряжение, ток и сопротивление. Поэтому важно постепенно, последовательно разобрать каждый раздел темы.