Квадратные уравнения

Квадратные уравнения входят в программу 8 класса по алгебре. Их решению посвящено большое количество учебных часов, а от усвоения принципов работы с ними, банального понимания, что перед вами именно квадратное уравнение учиться становится проще и интереснее. Рассмотрим особенности решения квадратных уравнений, алгоритмы, а также предложим несколько онлайн-калькуляторов, которые помогут закрепить принцип решения, проверить ответы.

Что такое квадратное уравнение?

Прежде чем говорить о квадратных уравнениях вспомним несколько других определений:

• Уравнение – равенство, которое содержит переменную. Значение этой переменной и нужно найти, чтобы равенство стало верным. Например, выражение вида X-4=12 является уравнением с переменной x.
• Корень уравнения – значение переменной, которой при подстановке в уравнение превратит его в верное числовое равенство. Например, если подставить в уравнение Х-4=12 значение Х=5, то мы получим выражение 5-4=12, что является не верным. Значит Х-5 не является корнем уравнения. А вот если подставить Х=16, то получится 16-4=12, а значит 16 – корень уравнения.
• Решить уравнение – это значит отыскать все его корни или доказать, что они не существуют.

Теперь поговорим о квадратных уравнениях. От представленного выше примера они отличаются своим видом. Его можно представить в виде: ax²+bx+c=0. В этом уравнении a является старшим коэффициентом, который не может равняться нулю, иначе уравнение не может считаться квадратным. b – второй коэффициент, а с – свободный член. Они оба могут равняться нулю.

Другими словами выражения вида:

• 4x²=0 (a=4, b=c=0)
• 2x²-3x=0 (a=2, b=-3, c=0)
• X²-4=0 (a=1, b=0, c=-4).

И подобные – являются квадратными.

У квадратных уравнений может быть два корня, один или вообще не быть корней. Для того, чтобы определить количество корней, необходимо вычислить дискриминант по формуле: D=b²-4ac.

Полученный дискриминант указывает на:

• отсутствие корней в уравнении, если D<0;
• уравнение имеет один корень, если D=0;
• 2 корня, если D>0.

Далее стоит углубиться в разные виды квадратных уравнений.

Приведенные и неприведенные квадратные уравнения

Приведенными уравнениями, называются те, у которых старший коэффициент (a) равен единице. Неприведенными – те, у которых старший коэффициент отличен от единицы.

Любое квадратное уравнение можно сделать приведенным, если разделить обе его части на старший коэффициент. Например:

1. Возьмем уравнение: 5х²-10х=125.
2. Разделим обе части на старший коэффициент – 5.
3. Получим: (5х²-10х):5=125:5.
4. Посчитаем: х²-2х=25.

Полные и неполные квадратные уравнения

Определение квадратных уравнений говорит о том, что a не должен равняться нулю. В случае, если коэффициент a=0, уравнение становится линейным и приобретает вид bx+c=0.

Если говорить о коэффициентах b и c, то они могут равняться 0, в том числе, и одновременно быть равны нулю. В этом случае уравнение называется неполным. Они как бы теряют слагаемое с неизвестной переменной или свободный член, или то и другое. Отсюда и получается их название – неполные.

Полное квадратное уравнение должно иметь все коэффициенты, отличные от нуля.

Решение неполных квадратных уравнений

Понятно, что существует 3 вида неполных квадратных уравнений: когда или второй коэффициент, или свободный член, или оба из них равны нулю. Рассмотрим подробнее как решаются каждый из этих видов уравнений.

Как решить уравнение ax² = 0

Если b и c равны нулю, то уравнение имеет вид ax² = 0. Такое уравнение всегда можно выразить в виде x² = 0. Для этого необходимо сделать уравнение приведенным, т.е. разделить обе его части на коэффициент a. У такого уравнения всего 1 корень, который всегда будет равен нулю. Других корней нет и быть не может (по свойству степени).

Иногда может потребоваться выполнить пошаговое решение даже такого простого уравнения. Предположим, что нужно вычислить корень уравнения 4x² = 0.

Пошагово решение выглядит так:

1. 4x² = 0
2. x² = 0.
3. х =
4. х=0
5. Ответ: х=0

Как решить уравнение ax² + с= 0

В таких неполных квадратных уравнениях коэффициент b = 0. Чтобы упростить уравнение, необходимо сделать 2 дополнительных шага:

1. Перенести с в правую часть: ax²=-c.
2. Сделать уравнение приведенным: x²=-c/a.

В случае, если правая часть уравнения отрицательная, то у него не будет корней. Это связано с тем, что квадрат любого числа не может давать в результате отрицательное число.

Если правая часть уравнения положительная, то можно использовать правило квадратного корня. Тогда у уравнения будет 2 корня (про это важно не забывать):

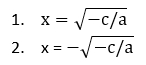
Пример:

1. 3х²-6=0
2. 3х²=6
3. х²=6:3
4. х²=2
5. 
   

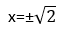
Ответ: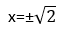 

Как решить уравнение ax² + bx = 0

Третий вид неполных квадратных уравнений, когда свободный коэффициент равен нулю. Его можно решить с помощью разложения на множители. Для этого:

1. Вынесем за скобки общий множитель х. Тогда уравнение будет иметь вид х(ах+b) = 0.
2. Получим совокупность двух уравнений х=0 и ах+b=0.
3. Найдем два корня. Первый уже известен, он равен нулю, а второй выражается в следующем виде: х=-b/a.

Пример:

1. 5х²+25х=0.
2. х(5х+25)=0.
3. х₁=0 и 5х+25=0.
4. Решаем линейное уравнение: 5х+25=0
5. х=-25/5
6. х=-5.

Ответ: х=0 и х=-5.

Дискриминант: формула корней квадратного уравнения

Для поиска корней квадратного уравнения существует формула корней:

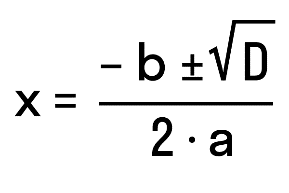
D=b²-4ac.

Для решения квадратного уравнения ax² + bx + с = 0 существует алгоритм.

Для начала, необходимо вычислить дискриминант по формуле D=b²-4ac. Затем:

• Если D<0, зафиксировать, что у уравнения нет действительных корней.
• Если D=0, то вычислить единственный корень уравнения по формуле х=-b/2a.
• Если D>0, то необходимо найти 2 действительных корня по формуле корней.

Формула Виета

В алгебре чаще всего квадратные уравнения решаются через формулу Виета. Теорема звучит следующим образом:

Сумма корней квадратного уравнения равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену. Это можно записать в следующем виде:

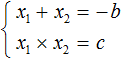
При этом значения х₁ и х₂ должны удовлетворять оба равенства.

Решим пример с использованием этой формулы:

x² - 6x + с = 0

Для начала запишем систему, соответствующую теореме Виета:

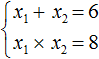
Эти два равенства позволяют подобрать подходящие корни, которые будут удовлетворять им. Проще всего подбирается вариант при умножении. 8 можно получить, если перемножить 4 и 2 или 1 и 8.

Однако эти значения должны удовлетворять и второму равенству, значит 1 и 8 не подходят, а вот сумма 4 и 2 = 6:

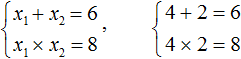
Следовательно числа 4 и 2 являются корнем уравнения x² - 6x + с = 0

Обзор онлайн-калькуляторов

В сети есть большое количество калькуляторов, которые позволяют не только получить ответ, но и полностью увидеть решение. Не стоит ими злоупотреблять, так как на экзамене вы не сможете ими воспользоваться. Они нужны, скорее, для самопроверки, поиска ошибок и закрепления материалов. Предлагаем познакомиться с самыми подробными онлайн-калькуляторами квадратных уравнений:

• OnlineMSchool – предлагает подробный онлайн калькулятор, который не только просто и быстро находит корни, но и дает пошаговое решение.
• Microsoft Math Solver – предлагает не только подробное решение квадратных уравнений и задач, но и позволяет выбрать вариант решения.
• Calc.by – неплохой калькулятор, рассчитанные только на поиск корней квадратных уравнений по формуле корней квадратного уравнения с графическим решением.

FAQ

Чем приведенные квадратные уравнения отличаются от неприведенных?

Приведенные квадратные уравнения имеют значение коэффициента a=1, а у неприведенных оно может отличаться.

Что такое неполные квадратные уравнения?

У неполных квадратных уравнений коэффициенты b и c могут быть равны нулю по отдельности или оба сразу.

Сколько корней может быть у квадратного уравнения?

Все зависит от того, чему равен дискриминант. В случае, если D<0 – корней нет. Если D=0 у уравнения 1 корень, D>0 – корней 2.

Вывод

Квадратные уравнения – большой раздел, которому посвящено много времени на уроках алгебры в 8 классе. Их достаточно просто решать, но важно помнить о том, что у них может быть разное количество корней, поэтому крайне важно правильно вычислять дискриминант. Формулы, которые используются при решении квадратных уравнений – достаточно простые, главное запомнить их. В остальном требуется побольше практики.