Формулы сокращённого умножения

Один из разделов алгебры за 7 класс изучает формулы сокращенного умножения. Тема достаточно сложная. Но важно разобраться с ней, так как подобные задания есть в тестах ЕГЭ. Понимание позволит проще проводить вычисления, уменьшая вероятность допустить при этом ошибку.

Формула сокращенного умножения – что это?

Такое название имеют формулы, используя которые можно сокращенно умножать или возводить в степень числа и многочлены. Поэтому расчеты проводятся быстрее, а запись получается компактнее. ФСУ в алгебре 7 класса применяют для упрощения математических выражений, разложения многочленов и их приведения к стандартному виду.

Существует 7 основных формул, которые рекомендуют запомнить школьникам.

Буквы можно заменять на числа, переменные, математические выражения.

На первый взгляд их очень сложно запомнить. Но, это не так. Достаточно воспользоваться методом аналогии. Если внимательно посмотреть на все эти формулы, то становится очевидным, что формула квадрата суммы напоминает формулу квадрата разности.

Аналогично можно запомнить разность квадратов и квадрат разности. Их формулы отличаются только знаком.

Дополнительные ФСУ

Для решения тестов на ЕГЭ также могут пригодиться несколько других не менее значимых тождеств.

Бином Ньютона

Формула, которую используют для разложения неотрицательной степени суммы двух переменных на разные слагаемые.

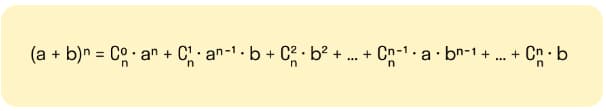
В качестве примера можно рассмотреть вычисление биноминальных коэффициентов, находящихся в строке n треугольника Паскаля:

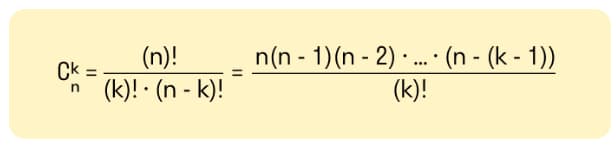
Формулы сокращенного умножения для квадрата и куба суммы и разности – отдельные случаи формулы бинома Ньютона при n=2 и n=3.

Формула возведения в квадрат 3 и более слагаемых

Ее можно использовать, если согласно условия в степень необходимо возвести 3 и более значений.

Формула разности n-х степеней слагаемых

Формула выглядит следующим образом:

aⁿ-bⁿ=(a-b)*(a^n-1+a^n-2*b+a^n-3*b²+…+a*b^n-2+b^n-1)

Если показатели четные, формула будет иметь следующий вид:

a^2*m-b^2*m=(a²-b²)*(a^2*m-2+a^2*m-4*b²+a^2*m-6*b⁴+…+b^2*m-2).

Если показатели нечетные, формула будет иметь следующий вид:

a^2*m+1-b^2*m+1=(a-b)*(a^2*m+a^2*m-1*b+a^2*m-2*b²+…+b^2*m).

Решение примеров

Потренируемся решать примеры:

1. (55+10)²

Чтобы решить пример, воспользуемся формулой квадрата сумма. Таким образом, получаем:

(55+10)²=55²+2*55*10+10²=3025+1100+100=4225.

2. Упростим выражение 64*с³-8

Чтобы решить пример, воспользуемся разностью кубов. Получаем: 64*с³-8=(4*с)³-2³=(4*с-2)((4*с)²+4*с*2+2²)=(4*с-2)(16*с²+8*с+4).

3. Раскроем скобки (7*у-х)*(7*у+х).

Решение может выглядеть несколькими способами:

• (7*у-х)*(7*у+х)=7*у*7*у+7*у*х-х*7*у+х*х=49*у²+7*у*х+7*у*х-х²=49* у²- х².
• Воспользуемся формулой сокращенного умножения: (7*у-х)*(7*у+х)=(7*у)²-х²=49* у²- х²

FAQ

Почему ФСУ изучают именно в 7 классе?

В 7 классе курс алгебры предусматривает изучение таких понятий, как многочлен и выполнение действий с ним. Поэтому формулы сокращенного умножения изучают именно тогда.

Когда были выведены ФСУ?

Известно, что люди в древнем Египте и Вавилоне пользовались данными формулами более 4 тысяч лет назад. Первая закономерность квадрата суммы была выведена Евклидом, который использовал геометрический способ выведения математических формул.

Где используют ФСУ?

Обычно их используют:

• в решении уравнений;
• при необходимости упростить выражение;
• для сокращения дробей;
• в случае умножения многочленов;
• для выделения квадрата двучлена, если в основе находится квадрат суммы.

Вывод

Зная формулы сокращенного умножения, решение многочленов становится намного проще. Достаточно последовательно выполнять каждое математическое действие и использовать представленные ФСУ.