Формулы приведения

Формулы приведения – это способ преобразования уравнений, который даёт возможность перейти от тригонометрических функций sin, cos, tg и ctg с углами π/2±α, π±α, 3π/2±α, 2π±α к аналогичным функциям угла α, который располагается в первой четверти единичной окружности. Тригонометрические формулы приведения упрощают решение, сводя всю работу к углам в пределе от 0 до 90 градусов.

Формулы приведения – список всех

Формулы приведения – это способ математического преобразования уравнений или выражений для упрощения их в более удобную форму. Этот метод широко применяется в математике, физике, инженерии и других науках для упрощения расчётов и анализа сложных систем.

Список формул приведения включает в себя различные математические тождества и преобразования. Некоторые из наиболее известных формул приведения включают в себя:

1. Тригонометрические формулы:
• (sin^2(x) + cos^2(x) = 1)
• (sin(2x) = 2sin(x)cos(x))
• (cos(2x) = cos^2(x) - sin^2(x))
2. Квадратные формулы:
• (a^2 - b^2 = (a + b)(a - b))
• ((a + b)^2 = a^2 + 2ab + b^2)
• - ((a - b)^2 = a^2 - 2ab + b^2)
3. Формулы приведения для степеней:
• ((a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3)
• ((a - b)^3 = a^3 - 3a^2b + 3ab^2 - b^3)

Доказательство формул

Доказательство формул приведения обычно основано на применении свойств математических операций, таких как раскрытие скобок, преобразование выражений и использование тригонометрических тождеств. Например, для доказательства тригонометрической формулы (sin(2x) = 2sin(x)cos(x)) можно воспользоваться формулой двойного угла для синуса: (sin(2x) = 2sin(x)cos(x)), где (sin(2x) = sin(x + x)) и затем применить формулу синуса суммы углов.

Таблица формул приведения

Формул приведения очень много и в этой таблице далеко не все из них. Поэтому необходимо научиться их выделять.

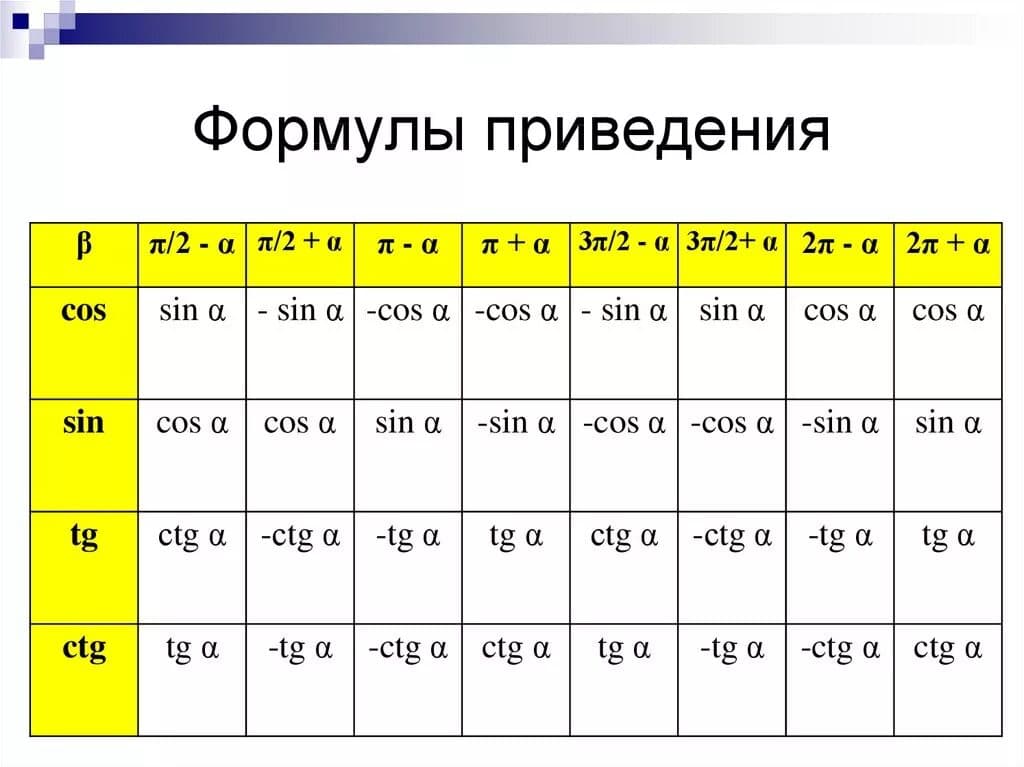
Пользоваться таблицей очень просто. В строках прописаны тригонометрические функции, в столбцах – выражения, от которых функции берутся. Выбираем пересечение строки и столбца и получаем нужный ответ. Например:

• cos(π/2+α)=−sin(α)

Как запомнить формулы приведения

Количество формул приведения огромно и запоминать их все нет смысла. Есть закономерности, позволяющие получать формулы приведения для различных углов и тригонометрических функций. Такие закономерности именуются мнемоническим правилом, иначе говоря, дают возможность легко и быстро запомнить сложные понятия. Мнемонический процесс запоминания тригонометрических формул приведения состоит из трёх частей.

Чтобы воспользоваться данным правилом, нужно выучиться определять знаки тригонометрических функций по четвертям единичной окружности.

Если вы непременно хотите выучить формулы приведения наизусть, то обратите внимание на методы, которые помогут в усвоении и запоминании математических тождеств:

• Сначала нужно понять, как выводятся формулы приведения. Разберитесь с доказательством каждой формулы, поймите логику и шаги, которые приводят к её получению. Это поможет лучше запомнить формулу.
• Можно попробовать связать формулу с чем-то знакомым или создать ассоциации для упрощения запоминания. Например, для формулы ((a + b)^2 = a^2 + 2ab + b^2) можно представить, что это похоже на раскрытие скобок при умножении двух выражений.
• Постоянное повторение и практика помогут закрепить формулы в памяти. Решайте много упражнений, используя формулы приведения, и проводите время над задачами разной сложности.
• Написание шпаргалки с формулами приведения, как и создание конспектов с объяснениями и примерами, может помочь в запоминании.

Запоминание формул приведения требует усилий и практики, но с помощью этих методов можно более эффективно учиться и запоминать.

FAQ

Как найти значение синуса и косинуса?

В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти. Если взять за основу определения, то возможно определить значения для определённого угла. Также можно вычислить значения тангенса и котангенса для определённого случая. Можно найти значение основных функций из тригонометрии для частных вариантов. Это углы: 0°, 90°, 180°, 270°, 360°.

Зачем нужны формулы приведения?

Формулы приведения – это соотношения, которые позволяют перейти от тригонометрических функций вида к функциям аргумента. С их помощью синус, косинус, тангенс и котангенс произвольного угла можно привести к синусу, косинусу, тангенсу и котангенсу угла из интервала от 0 до 90 градусов (от 0 до радиан). Формулы приведения позволяют нам переходить к работе с углами в пределах 90 градусов.

Что такое формулы приведения в тригонометрии кратко?

Формулы приведения – это соотношения, с помощью которых значения тригонометрических функций аргументов выражаются через значения sinα, cosα, tgα, ctgα.

Что такое тригонометрические тождества?

Тригонометрические тождества — математические выражения для тригонометрических функций, выполняющиеся при всех значениях аргумента (из общей области определения).

Вывод

• Формулы приведения играют важную роль в тригонометрии, математике и других науках, облегчая анализ и решение задач.
• Их доказательства основаны на математических преобразованиях и свойствах операций.
• Формул очень много и учить их все наизусть не обязательно. Нужно знать мнемоническое правило, которое позволяет быстро вывести необходимую формулу.