Арксинус и уравнение sin x = a

Рассмотрим понятие функции арксинус и пример вычисления арксинусов по графику на единичной окружности через уравнение sin x = a при .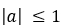

Согласно теореме о существовании обратной функции, прямая функция sin x = a должна быть непрерывной.

Понятие арксинуса

В уравнении y = sin x, аргумент x — значение угла в градусах или радиане, а y — синус угла, значение которого определяется в пределах |-1;1|. По заданному синусу определяется угол. Но 1 значению sin соответствует неопределенное количество углов. Например, при sin x = 1, то 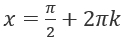, k ∈ Z. Если sin x = 0, то 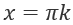, k ∈ Z.

Таким образом, для построения обратной функции значения углов ограничивают отрезком, на котором sin в пределах |-1;1|, но только 1 раз: .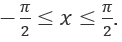

Значит, арксинусом числа 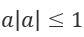 называют такое число 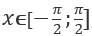, и sin = a.

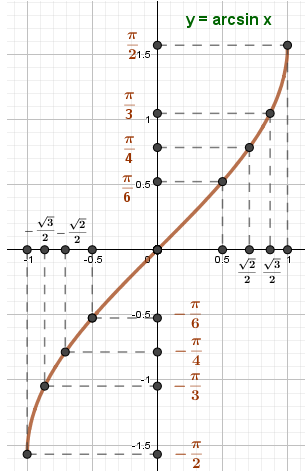
График и свойства функции y = arcsin x

Область определения 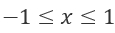, а значит функция ограничена сверху и снизу значениями 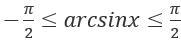, где y находится в пределах .

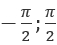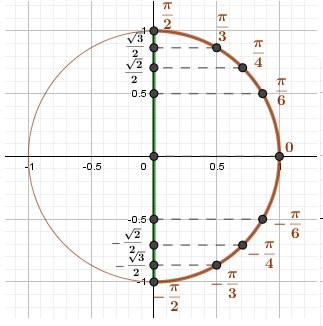
Функция возрастает и непрерывна на области определения и является нечетной arcsin(-x) = - arcsin(x).

Уравнение sin x = a

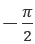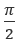Значения arcsin могут быть только углы со значениями от  до  (от -90°до 90°). Углы левой части окружности определяют как разность между  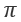и arcsin угла правого полушария. Углы, которые больше установленных значений  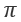записывают через сумму arcsin и разницы, на которую выявлено превышение.

Рассмотрим на примере. Решим уравнение .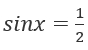

Порядок решения:

1. Построим перпендикулярную линию через точку 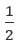 на оси OY. Прямая пересечет окружность в 2 точках, образующих углы  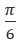и 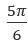. Значения углов одновременно выступают базовыми корнями.
2. Определим корень уравнения. К корню справа 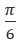 прибавим полный оборот 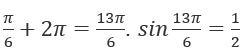, а значит  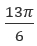тоже является корнем уравнения. И также корнями будут все другие углы вида 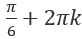. Притом количество оборотов полных или добавленных неограниченно. Углы вида  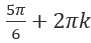тоже корни.
3. Определим значение уравнения. 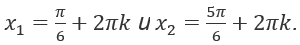Если 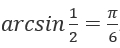. Запишем ответ: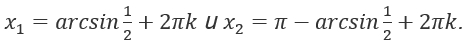 
   
   

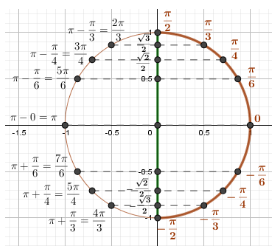
Рассмотрим еще одно решение уравнения sinx = 0,8

Чтобы найти значение уравнения на оси синусов OY требуется построить горизонталь, проходящую перпендикулярно через точку 0,8. Линия пересечет окружность в 2 точках.

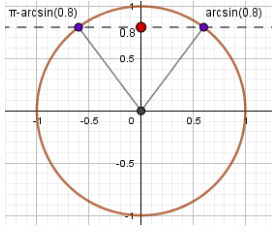
Правая точка образует угол равный arcsin0,8, а левая — разность разверного угла и арксинуса .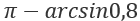

Сумма или разность полных оборотов к каждому из значений даст другие корни:

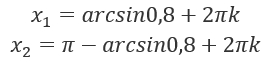
Если 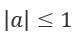, уравнение sinx = a равно:

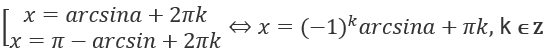
Если 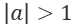, уравнение у уравнения отсутствует.

FAQ

Что такое тригонометрическое уравнение?

Уравнение, которое содержит переменную под знаком тригонометрической функции. Уравнение вида sinx = a — простейшее тригонометрическое уравнение.

Если sinx = 0, 1 и -1 как определить значение x

Для любого a∈ [−1;1] справедлива формула arcsin(-1) = -arcsina

Случаи-исключения, при k ∈ Z:

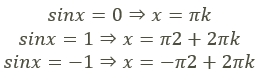
Для понимания темы требуется ежедневно практиковаться, особенно если необходимо подготовиться к сдаче ОГЭ или ЕГЭ. Разбирайте готовые примеры с решениями в интернет и запишитесь на курсы подготовки.