Арифметическая прогрессия

Арифметической прогрессией называют последовательность чисел, где каждый последующий член больше или меньше предыдущего на одно и то самое число. Разность между двумя идущими друг за другом членами, называют разностью арифметической прогрессии. Для ее определения можно воспользоваться формулой:

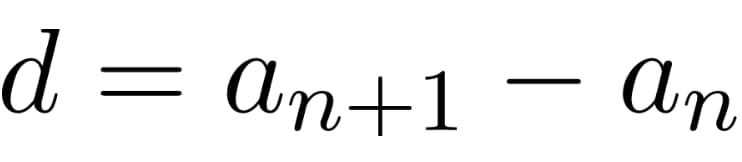
Если по условию нам известен первый и n-й член, то чтобы найти разность используют следующую формулу:

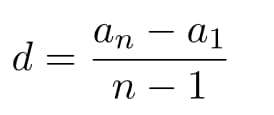
Разновидности арифметических прогрессий

Выделяют 3 вида арифметических прогрессий:

1. Возрастающая. В данном случае разность всегда будет положительным значением. К примеру, 10, 15, 20, 25, 30… - данная прогрессия возрастающая, так как d=5, а это больше нуля.
2. Убывающая. В такой арифметической прогрессии разность является отрицательным числом. К примеру, 50, 45, 40, 35 ,30, 25… - данная прогрессия убывающая, поскольку d=-5, а это меньше нуля.
3. Стационарная. В данном случае разность арифметической прогрессии будет равняться нулю. К примеру, 25, 25, 25, 25, 25… - данная прогрессия стационарная, поскольку d=0.

Основные свойства арифметической прогрессии

Основным свойством, которым обладает каждая арифметическая прогрессия является то, что каждый из ее членов, начиная со второго и выше, равняется средне арифметическому значению членов, которые стоят рядом с ним (перед и после).

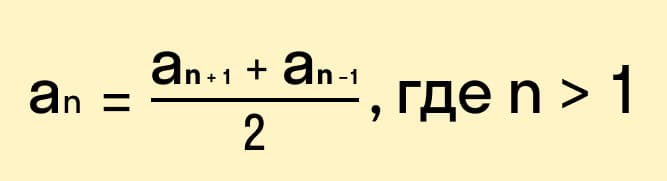
Формула n-го члена любой арифметической прогрессии выглядит следующим образом:

Из этого следует, что зная первый член и значение разности арифметической прогрессии, мы легко можем найти каждый из ее членов, независимо от его порядкового номера.

Основные формулы арифметической прогрессии выглядят следующим образом.

Примеры арифметической прогрессии

Рассмотрим данную тему на конкретных примерах.

Пример 1. Необходимо найти разность арифметической прогрессии 12, 7, 2.

Чтобы ее найти, необходимо воспользоваться формулой d = a_n+1 –a_n.

Отсюда: d = 12-7=5

Ответ: 5.

Пример 2.

FAQ

Чем отличаются арифметическая и геометрическая прогрессии?

В арифметической каждый следующий член прогрессии отличается от предыдущего на одно и то самое число. В геометрической он отличается в определенное количество раз.

В чем польза арифметической прогрессии?

Арифметическая прогрессия представляет собой числовой ряд, в котором между двумя последовательными членами существует общее различие. В повседневной жизни ее можно использовать при необходимости обобщения набора шаблонов. К примеру, ожидая на автобусной остановке транспорт, мы можем предположить, что автобусы ходят с постоянной скоростью и определенной периодичностью. Таким образом, мы можем рассчитать, во сколько приедет следующий.

Вывод

Арифметическая прогрессия представляет собой определенный числовой ряд, в котором числа увеличиваются или уменьшаются на одно и то же число. Для определения разности или суммы арифметической прогрессии, ее n-го члена и т. д. существуют специальные формулы, рассмотренные выше.